Wolfram Alpha doesn't give $-2$ for $(-8)^{1/3}$, and it absolutely fails to draw $f(x)=x^{1/3}$ - does anyone know why? Am I missing something very 'deep' Wolfram Alpha is trying to teach me?
Here's what the graph should look like:
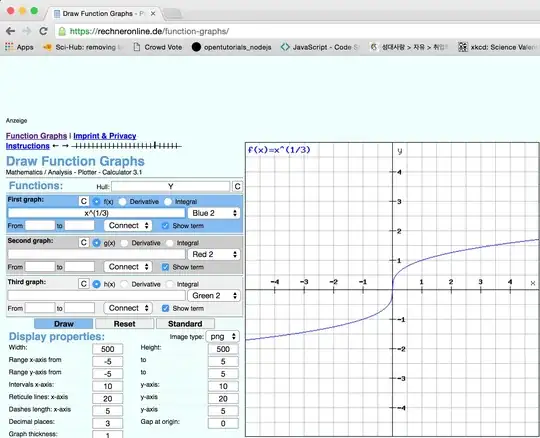
And here's what Wolfram Alpha draws:
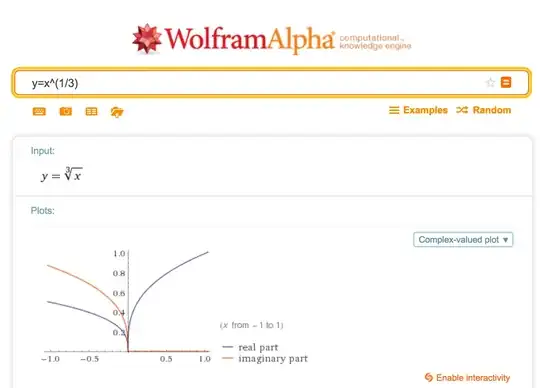
cbrt(x)for the cube root function in Wolfram|Alpha, which (as implemented in that particular piece of software) is different from $x^{1/3}$. – Mark McClure Mar 11 '16 at 12:56