Integral $\int_0^1 \frac{\ln|1-x^a|}{1+x}\, dx$

Question

Let's consider this integral:

$$g(a)=\int_0^1 \frac{\ln|1-x^a|}{1+x}\, dx$$

There is a related integral, which is more widely known. See this question, this question and this paper.

$$f(a)=\int_0^1 \frac{\ln(1+x^a)}{1+x}\, dx$$

It has a number of interesting properties, namely:

$$f(a)-f(-a)=-\frac{\pi^2}{12} a$$

$$f(a)+f \left( \frac{1}{a} \right)=\ln^2 2$$

We can immediately see (by evaluating the integral as well):

$$f(0)=\ln^2 2$$

$$f(1)=\frac{\ln^2 2}{2}$$

In the related paper the way is shown to get a closed form for infinitely many values of $a$.

---

Now we consider $g(a)$. Notice the important limit:

$$\lim_{a \to \pm 0} g(a)=-\infty$$

In this answer it is shown that:

$$g(1)=\int_0^1 \frac{\ln(1-x)}{1+x}\, dx=\frac{\ln^2 2}{2}-\frac{\pi^2}{12}$$

I have not been able to find references about the general integral yet. However, the most interesting property is this obvious formula:

$$g(2a)=g(a)+f(a)$$

Using it, we can find some values without explicitly evaluating the integral.

$$g(2)=g(1)+f(1)=\ln^2 2-\frac{\pi^2}{12}$$

This integral also has the same symmetry relation as $f(a)$:

$$g(a)-g(-a)=-\frac{\pi^2}{12} a$$

However, I have not been able to find any formula for $g(1/a)$ (the proof used for $f(a)$ fails because of the singularity at $a=0$).

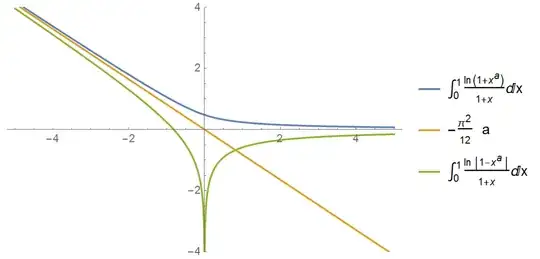
Here is a plot of these two integrals and their common asymptote:

And here is a list of 'nice' values for $f(a)$ and $g(a)$ for integer $a$:

$$ \begin{matrix} a & f(a) & g(a) \\ -4 & & \dfrac{11 \pi ^2}{48}+\dfrac{21 \ln ^2 2}{12} \\ -2 & \dfrac{7 \pi ^2}{48}+\dfrac{3 \ln ^2 2}{4} & \dfrac{\pi ^2}{12}+\ln ^2 2 \\ -1 & \dfrac{ \pi ^2}{12}+\dfrac{\ln ^2 2}{2} & -\dfrac{\ln ^2 2}{2} \\ -\dfrac{1}{2} & \dfrac{\pi ^2}{16}+\dfrac{\ln ^2 2}{4} & -\dfrac{ \pi ^2}{16}+\dfrac{\ln ^2 2}{4} \\ 0 & \ln ^2 2 & -\infty \\ \dfrac{1}{2} & \dfrac{\pi ^2}{48}+\dfrac{\ln ^2 2}{4} & -\dfrac{5 \pi ^2}{48}+\dfrac{\ln ^2 2}{4} \\ 1 & \dfrac{\ln ^2 2}{2} & -\dfrac{ \pi ^2}{12}+\dfrac{\ln ^2 2}{2} \\ 2 & -\dfrac{\pi ^2}{48}+\dfrac{3 \ln ^2 2}{4} & -\dfrac{ \pi ^2}{12}+\ln ^2 2 \\ 4 & & -\dfrac{5 \pi ^2}{48}+\dfrac{21 \ln ^2 2}{12} \\ \end{matrix} $$

I was able to find most of these values using the highlighted relations, only checking with Mathematica after the fact.

Can we find more closed form expressions for $g(a)$ for some $a$, maybe using the values for $f(a)$ (see the linked paper)?

What other properties of $g(a)$ can we obtain?

And what is the one real solution of $g(a)=0$ (see the plot)?

---

Also for any $a>0$ we can define $g(a)$ in terms of $f$:

$$g(a)=g(2a)-f(a)=g(4a)-f(a)-f(2a)=g(8a)-f(a)-f(2a)-f(4a)$$

$$\lim_{a \to + \infty} g(a)=\lim_{a \to + \infty} f(a)=0$$

$$g(a)=- \sum_{k=0}^{\infty} f(2^k~a), ~~~~~ a>0$$

The last relation also directly follows from the well-known identity:

$$\prod_{k=0}^{\infty} \left( 1+x^{2^k} \right)=\frac{1}{1-x}, ~~~~~|x|<1$$

---

We can also use $f(a)$ and $g(a)$ to define a whole family of integrals:

$$\sum_{k=0}^{n-1} x^{ka}=\frac{1-x^{na}}{1-x^a}$$

$$I_n (a)=\int_0^1 \ln \left( \sum_{k=0}^{n-1} x^{ka} \right) \frac{dx}{1+x}=g(na)-g(a)$$

$$J_n (a)=\int_0^1 \ln \left( \sum_{k=0}^{n-1} (-1)^k x^{ka} \right) \frac{dx}{1+x}= \begin{cases}g(na)-f(a) & n=2j \\ f(na)-f(a) & n=2j+1 \end{cases} $$

For example:

$$\int_0^1 \frac{\ln(1+x+x^2+x^3)}{1+x}\, dx=g(4)-g(1)=-\dfrac{\pi ^2}{48}+\dfrac{15 \ln ^2 2}{12}$$

Answer 1

Here are two asymptotics:

• When $a \to 0^+$, we can use the substitution $x = e^{-u}$ to write $$ g(a) = \int_{0}^{\infty} \frac{\log (1 - e^{-au})}{e^u + 1} \, du = \int_{0}^{\infty} \frac{\log a}{e^u + 1} \, du + \int_{0}^{\infty} \frac{\log \left( \frac{ 1 - e^{-au}}{a} \right)}{e^u + 1} \, du. $$ It is not hard to check that the last integral is dominated by some integrable function, thus in view of the dominated convergence theorem, we have $$ g(a) = \log 2 \log a + \int_{0}^{\infty} \frac{\log u}{e^u + 1} \, du + o(1) = \log 2 \log a - \frac{1}{2}\log^2 2 + o(1) \quad \text{as } a \to 0^+. $$

• When $a \to \infty$, we first perform integration by parts to write $$ g(a) = \int_{0}^{1} \frac{ax^{a-1}}{1 - x^a} \log\left( \frac{1+x}{2} \right) \, dx. $$ Applying the substitution $x = e^{-u/a}$ and introducing a new function $h(x) = -\frac{2}{x}\log(\frac{1+e^{-x}}{2})$, we can write $$ g(a) = -\frac{1}{2a} \int_{0}^{\infty} \frac{u h(u/a)}{e^u - 1} \, du. $$ Since $h$ is uniformly bounded on $[0, \infty)$ and $h(x) \to 1$ as $x \to 0^+$, by the dominated convergenc theorem again we have $$ g(a) = -\frac{1 + o(1)}{2a} \int_{0}^{\infty} \frac{u}{e^u - 1} \, du = -\frac{\zeta(2) + o(1)}{2a} \quad \text{as } a \to \infty. $$