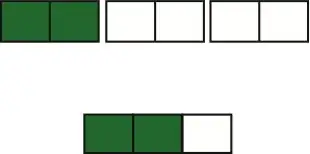
Want to visualize rule division of fraction.
For example
1)
2 2 4
_ * _ = _
2 3 6
in this case we "split" each piece of cake in numerator to the 2 "first fraction" and apply the same operation for the denominator.
Could you please clarify rule with devision, why we should turn fractions and multiply it. How can I visualize this rule?
Thanks.
Here's a good way to think about it. When you divide $6$ by $2$, you're asking how many groups of $2$ apples make up $6$ apples. The answer, of course, is that there are $3$ groups.
Now, when you want to divide $1$ by $2/3$, you're asking how many groups of $2/3$ of a cup there are in $1$ cup. As the second picture clearly shows, there are $1 1/2$ or $3/2$ groups. This same principle generalizes for any fraction division.
Think of it this way:$$a\div b=\frac{a}{b}=\frac{a}{1}\times\frac{1}{b}=a\times\frac{1}{b}$$Now lets set:$$a=\frac{p}{q}, b=\frac{r}{s}$$We then get:$$\frac{p}{q}\div\frac{r}{s}=\frac{p}{q}\times\frac{1}{\frac{r}{s}}=\frac{p}{q}\times\frac{s}{r}$$
This depends on you knowing that:$$\frac{1}{\frac{r}{s}}=\frac{s}{r}$$This can be shown by first letting:$$\frac{1}{\frac{r}{s}}=x\tag{1}$$and then multiplying both sides by $\frac{r}{s}$ to get:$$\require{cancel}\frac{1}{\cancel{\frac{r}{s}}}\times\frac{\cancel{\frac{r}{s}}}{1}=x\times\frac{r}{s}$$$$\therefore 1=x\times\frac{r}{s}$$Now just multiply both sides by $\frac{s}{r}$ to get:$$\require{cancel}1\times\frac{s}{r}=x\times\frac{\cancel{r}}{\cancel{s}}\times\frac{\cancel{s}}{\cancel{r}}=x$$$$\therefore x=\frac{s}{r}$$ Now substitute this back into (1) to get:$$\frac{1}{\frac{r}{s}}=x=\frac{s}{r}$$
If you accept the multiplication rule, then you must also accept the division rule. If you accept that any division sentence can be restated as a multiplication sentence, then we can agree that. $$t = \frac{r}{s}\div \frac{p}{q}$$ $$t\times\frac{p}{q} = \frac{r}{s}$$ $$(t\times\frac{p}{q})\times\frac{q}{p} = \frac{r}{s}\times\frac{q}{p}$$ $$t\times(\frac{p}{q}\times\frac{q}{p}) = \frac{r}{s}\times\frac{q}{p}$$ $$t\times\frac{pq}{qp} = \frac{r}{s}\times\frac{q}{p}$$ $$t\times\frac{pq}{pq} = \frac{r}{s}\times\frac{q}{p}$$ $$t\times 1 = \frac{r}{s}\times\frac{q}{p}$$ $$t = \frac{r}{s}\times\frac{q}{p}$$ My personal favorite is to turn the division into a fraction (because I looooove fractions). $$t = \frac{r}{s}\div\frac{p}{q}=\frac{\frac{r}{s}}{\frac{p}{q}}$$ Now, just multiply by one (and recall that anything divided by itself is one). $$\frac{\frac{r}{s}}{\frac{p}{q}} = \frac{\frac{r}{s}}{\frac{p}{q}}\times\frac{\frac{q}{p}}{\frac{q}{p}} = \frac{\frac{r}{s}\times\frac{q}{p}}{\frac{p}{q}\times\frac{q}{p}}=\frac{\frac{r}{s}\times\frac{q}{p}}{\frac{pq}{qp}}=\frac{\frac{r}{s}\times\frac{q}{p}}{1}=\frac{r}{s}\times\frac{q}{p}$$
To make this a bit more concrete, suppose that you know the area of a rectangle and one of its dimensions. How would you find the other dimension? I think that the most logical thing to do would be to take the formula $W=A/L$ and restate it as $A=L\times W$.
