Why does $\binom{n}{2} =[ (n-1) + (n-2) + (n-3)+\cdots +1]$?

Question

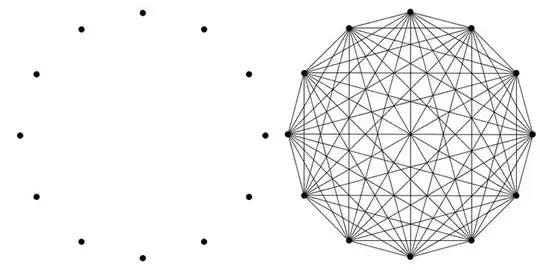
I was recently doing a homework problem that involved finding the number of lines used to connect a given number of points on a circle. Looking at it logically, I saw that that for the first point, there would be $n-1$ lines you could draw (where $n$ is the number of points on the circle) and the next point would have $n-2$ lines because you're not repeating the line between point $1$ and point $2$. It made sense that this would continue until point $n$, at which point there would be zero lines you can draw.

This meant that if you just add up all of those, you'd get the number.

For example, in the picture below there are $12$ points, so

$11+10+9+8+7+6+5+4+3+2+1 = 66$ lines.

That's all fine, but the weird thing was, when I looked in the back of the book, the answer was given as $\binom{n}{2}$, which also equals $66$. What's the relationship? Why are the two equal?

Answer 1

$$\sum_{k=0}^n k = \frac{(n+1)n}{2}$$

And

$$\binom nk = \frac{n!}{k!(n-k)!} = \frac{n\cdot(n-1)\cdots(n-k+1)}{k!}$$

In particular

$$\binom n2 = \frac{n(n-1)}{2} = \sum_{k=0}^{n-1} k$$

Another way to see it is by induction. In particular $\binom 1 2 = 0$, and $\binom {n+1}{2} = \binom{n}{1} + \binom{n}{2}$, which probably makes the identity seem a bit less "random".

Answer 2

You have $\binom n 2 = \frac{n(n-1)}2$. Now, a famous formula says that $$ \sum_{k=1}^{n-1}k = \frac{n(n-1)}2. $$ This can be proved by induction. To understand it - at least when $n$ is odd - write $$ 1 + \ldots + (n-1) = (1 + (n-1)) + (2 + (n-2)) + \ldots, $$ which is $(n-1)/2$ times $n$.

Answer 3

SBareS has provided you with a good answer. Here is a combinatorial proof.

There are $\binom{n}{2}$ subsets of $\{1, 2, 3, \ldots, n\}$ with two elements. Of these subsets, there are $k - 1$ subsets with largest element $k$, with $1 \leq k \leq n$. Hence, $$\sum_{k = 1}^{n} (k - 1) = \binom{n}{2}$$

In the problem you did, think of the vertices as numbered. You counted the diagonals in which the vertex with the smaller number was $k$, with $1 \leq k \leq 12$. That yields the sum $$\sum_{k = 1}^{12} (12 - k) = 11 + 10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 66$$ Notice that $$\sum_{k = 1}^{n} (n - k) = \sum_{k = 1}^{n} (k - 1) = \binom{n}{2}$$ since the summands are the same, just written in the opposite order.

Answer 4

A way to get the result stated directly is to note that if you have $n$ vertices, to pick a diagonal is to select a pair of vertices, which means in all there are $\binom{n}{2}$ diagonals.

Another way is to pick each of the $n$ vertices, it participates in $n - 1$ diagonals connecting it to the other vertices, thus $n (n - 1)$ in all. But this counts each diagonal twice, once for each of its ends. Thus $n (n - 1) / 2 = \binom{n}{2}$

Answer 5

You just explained it.

Say you have a mixture of blue and white balls. You draw 11 and two of them are blue. How many ways might the two blue balls be arranged?

If the first ball is in position 1, the other ball might be in any of the other 10 positions. If the first ball is in position 2, the second ball may be in any of 9 positions because you don't double count the {1,2} combination which had the first ball in position 1. And so on. It may be easier to ser that the triangular sum equals the conbination function when you use balls. But tge lines are being counted the same way.

Answer 6

Order the elements of $N={1,...,n}$. There are obviously n-1 two element subsets containing 1. We have counted all the subsets containing 1, so remove 1 from $N$. Now there are obviously n-2 two element subsets contining 2 in $N/{1}$. Rinse and repeat until you have exhausted the set.