Finding Maximum Area of a Rectangle in an Ellipse

Question

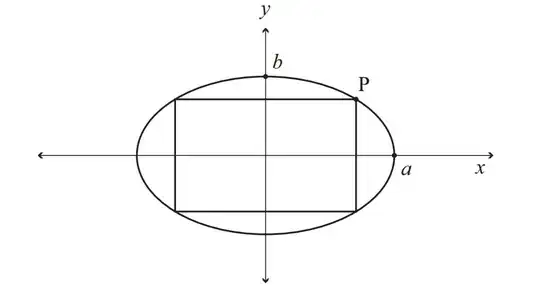
Question: A rectangle and an ellipse are both centred at $(0,0)$. The vertices of the rectangle are concurrent with the ellipse as shown

Prove that the maximum possible area of the rectangle occurs when the x coordinate of point $P$ is $x = \frac{a}{\sqrt{2}} $

---

What I have done

Let equation of ellipse be

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

Solving for y

$$ y = \sqrt{ b^2 - \frac{b^2x^2}{a^2}} $$

Let area of a rectangle be $4xy$

$$ A = 4xy $$

$$ A = 4x(\sqrt{ b^2 - \frac{b^2x^2}{a^2}}) $$

$$ A'(x) = 4(\sqrt{ b^2 - \frac{b^2x^2}{a^2}}) + 4x\left( (b^2 - \frac{b^2x^2}{a^2})^{\frac{-1}{2}} \times \frac{-2b^2x}{a^2} \right) $$

$$ A'(x) = 4\sqrt{ b^2 - \frac{b^2x^2}{a^2}} + \frac{-8x^2b^2}{\sqrt{ b^2 - \frac{b^2x^2}{a^2}}a^2} = 0 $$

$$ 4a^2\left(b^2 - \frac{b^2x^2}{a^2} \right) - 8x^2b^2 = 0 , \sqrt{ b^2 - \frac{b^2x^2}{a^2}a^2} \neq 0 $$

$$ 4a^2\left(b^2 - \frac{b^2x^2}{a^2} \right) - 8x^2b^2 = 0 $$

$$ 4a^2b^2 - 4b^2x^2 - 8x^2b^2 = 0 $$

$$ 4a^2b^2 - 12x^2b^2 = 0 $$

$$ 12x^2b^2 = 4a^2b^2 $$

$$ x^2 = \frac{a^2}{3} $$

$$ x = \frac{a}{\sqrt{3}} , x>0 $$

Where did I go wrong?

edit:The duplicate question is the same but both posts have different approaches on how to solve it so I don't think it should be marked as a duplicate..

Answer 1

Its easier to solve this question using parametric points.

Let one vertex of the rectangle be $(a\cos\theta,b\sin\theta)$.

The other vertices are $(a\cos\theta,-b\sin\theta)$, $(-a\cos\theta,b\sin\theta)$, $(-a\cos\theta,-b\sin\theta)$

The area of rectangle formed is $$A(\theta)=4ab\cos\theta\sin\theta=2ab\sin2\theta$$

Maximum area is $2ab$ and it occurs when $\theta=\frac{\pi}{4}$ (or when $\sin2\theta$ is maximum).

When $\theta=\frac{\pi}{4}$, $x$-coordinate $=a\cos\frac{\pi}{4}=\frac{a}{\sqrt{2}}$

Answer 2

Your mistake is here $$ A'(x) = 4(\sqrt{ b^2 - \frac{b^2x^2}{a^2}}) +\color{red}{\frac12} \times4x\left( (b^2 - \frac{b^2x^2}{a^2})^{\frac{-1}{2}} \times \frac{-2b^2x}{a^2} \right). $$

Answer 3

Let equation of ellipse be

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$

Solving for y

$$ y = \sqrt{ b^2 - \frac{b^2x^2}{a^2}} $$

Let area of a rectangle be $4xy$

$$ A = 4xy $$

$$ A = 4x(\sqrt{ b^2 - \frac{b^2x^2}{a^2}}) $$

$$ A'(x) = 4(\sqrt{ b^2 - \frac{b^2x^2}{a^2}}) + 4x\left( (b^2 - \frac{b^2x^2}{a^2})^{\frac{-1}{2}} \times \frac{-b^2x}{a^2} \right) $$

$$ A'(x) = 4\sqrt{ b^2 - \frac{b^2x^2}{a^2}} + \frac{-4x^2b^2}{\sqrt{ b^2 - \frac{b^2x^2}{a^2}}a^2} = 0 $$

$$ 4a^2\left(b^2 - \frac{b^2x^2}{a^2} \right) - 4x^2b^2 = 0 , \sqrt{ b^2 - \frac{b^2x^2}{a^2}a^2} \neq 0 $$

$$ 4a^2\left(b^2 - \frac{b^2x^2}{a^2} \right) - 4x^2b^2 = 0 $$

$$ 4a^2b^2 - 4b^2x^2 - 4x^2b^2 = 0 $$

$$ 4a^2b^2 - 8x^2b^2 = 0 $$

$$ 8x^2b^2 = 4a^2b^2 $$

$$ x^2 = \frac{a^2}{2} $$

$$ x = \frac{a}{\sqrt{2}} , x>0 $$

The mistake is in third step while differentiating.

differentiating $\sqrt x$ will give you $\frac{1}{2\sqrt x}$

Answer 4

The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. This transformation multiplies areas by the constant $\dfrac{a}{b}$, so the problem is equivalent to finding the rectangle of maximum area in a circle, which is well-known to be a square.

Or, looked at another way (pun intended), this ellipse is what you see if you look at the circle of radius $a$ in the $x-y$ plane from just the right angle instead of from directly above. When you see what appears to be an inscribed rectangle in the ellipse of maximum area, what you’re looking at is an inscribed rectangle in the circle of maximum area.