Geometrical proof of the limit $\lim_{(x \to 0)}\left(\frac{e^x-1}{x}\right)=1$ using sandwich theorem.

Question

I am studying about sandwich theorem and its applications by deriving some well-known limits such as this- $$\lim_{(x \to 0)}\left(\frac{e^x-1}{x}\right)=1$$ while I found some proofs of this result by first defining $e$ and then using that definition such as here(Proof of $ f(x) = (e^x-1)/x = 1 \text{ as } x\to 0$ using epsilon-delta definition of a limit)(which I agree sounds a lot easier because if one is using the Taylor series expansion of $e^x$ then it becomes very easy)but my book tries to do this in a different manner by using this inequality $$\frac{1}{1+|x|}≤\left(\frac{e^x-1}{x}\right)≤ 1 + (e – 2) |x|$$(holds for all $x$ in $[–1, 1]-[0]$)

and then just using sandwich theorem the limit is easily calculated , but the book does not explain as to from where this inequality came from.And I am not able to get it by myself ,as I am not able to see how can this result be so obvious, and even though the graph does make it a bit clear(which I have attached below) still I am not able to get the given inequality(any hints there?)

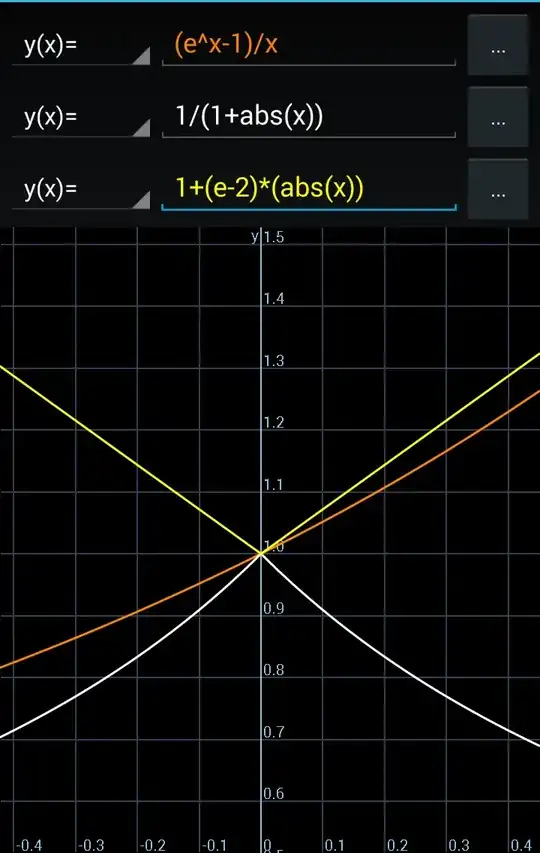
I tried to search it on this site but couldn't find it,but still I found some very neat applications of sandwich theorem such as here ( How to prove that $\lim\limits_{x\to0}\frac{\sin x}x=1$?) so which makes me think that maybe this inequality can be derived easily by looking at it's geometrical interpretation such as in the link given.

---

So can someone please help me in understanding the geometrical meaning of this inequality (just like in the limit given in the link above) or help to derive it using its geometrical implications?

---

1)And even if that is not possible can someone help me in understanding the inequality intuitively because I honestly haven't got any idea as to how such a weird looking inequality can be related to the given limit,

2)And how that inequality is derived ?

3)Also what can possibly be the motivation behind this complicated inequality for deriving this limit, are there other such wierd inequalities also for finding this limit?

Answer 1

This is a response to OP's comments which is a bit long for a comment.

---

As I iterated in my comments to the question, the evaluation of limit of $(e^{x} - 1)/x$ as $x \to 0$ crucially depends on the definition of the symbol $e^{x}$. There are multiple approaches to define $e^{x}$ (which are provided here, here and here). One of these approaches is based on defining logarithm as an integral and treating exponential function as its inverse.

OP raises a further doubt about some sort of circularity involved here. His argument is that the concept of integrals is itself dependent on that of limits and hence something based on integrals should not be used as a basis to establish a certain limit. However it should be made clear that there is absolutely no circularity involved if we define $$\log x = \int_{1}^{x}\frac{dt}{t}$$ and further define $e^{x} = y$ if $x = \log y$. This is because the definition of $\log x$ as an integral is not dependent on any particular properties or features of $e^{x}$ (in particular the limit of $(e^{x} - 1)/x$ as $x \to 0$. The definition of $\log x$ is based on the properties of function $1/x$ and the concept of definite integrals as a limit of sum (thus the definition of $\log x$ is based on concept of limits).

On the other hand if one wishes to avoid the integrals (because from OP's point of view integrals come much later in study of calculus compared to limits) then we can directly use limits to define $e^{x}$ as follows $$e^{x} = \lim_{n \to \infty}\left(1 + \frac{x}{n}\right)^{n}$$ and using this definition we can easily prove that $\lim\limits_{x \to 0}\dfrac{e^{x} - 1}{x} = 1$.

Note however that such proofs can be daunting both for students (and teachers alike to explain) in a first course of calculus (meaning students are of age 16-17 years). It is preferable to be a bit honest and instead of hand waving introduce the functions $\log x, e^{x}, a^{x}$ with a list of their properties including the following standard limits $$\lim_{x \to 0}\frac{\log(1 + x)}{x} = 1 = \lim_{x \to 0}\frac{e^{x} - 1}{x},\, \lim_{x \to 0}\frac{a^{x} - 1}{x} = \log a$$ and mention that these properties can/will be proved in a later course on advanced calculus/real analysis.

However I have seen that most instructors almost always prefer hand waving instead of deferring the rigorous approach to later courses. This is one of reasons many students feel confused (OP seems to be a genuine victim of such intellectual fraud because his textbook author has the audacity to prove the limit of $(e^{x} - 1)/x$ via squeeze theorem without a definition of $e^{x}$).

Answer 2

i am not sure if we are allowed to use integrals, if we are, then using the mean value theorem for integrals, i can write $$ \frac{1-e^x}{x} = \frac 1x\int_0^x e^t \, dt = e^{\theta x} \text{ for some $0 < \theta < 1$}.$$ we now use the fact that $e^{\theta x}$ is between $e^x$ and $1$ to conclude the limit as $x$ tend to $0$ is $1$ using the squeeze theorem.

p.s.: i can prove the inequality $$f(x) = \frac x{x+1} \le e^x - 1 = g(x)$$ by showing that $g$ is concave up and $f$ is concave down. we also have one common tangent $y = x$ at $x = 0, y = 0$ which gives us $$\frac x{x+1} \le x \le e^x - 1 $$ equality iff $x = 0.$

i can show the other inequality too. we will only need to show for $x > 0$ that $$h(x) = e^x-1 \le x + bx^2 = j(x)$$ we know that the graph of $h$ will cross the graph of $j.$ we just choose $b$ so that they cross at $x = 1.$ that means $e-1 = 1 + b$ which gives you the value for $b = e-2.$

Answer 3

Just playing around to see what happens.

If $e(x+y) =e(x)e(y) $ with $e'(0) = 1$, then $e(x+h) =e(x)e(h) $ so $e(x+h)-e(x) =e(x)(e(h)-1) $ so, letting $h \to 0$ and using $e(0) = 1$, $e'(x) =e(x)e'(0) =e(x) $.

Therefore, $e(x)-1 =\int_0^x e(t) dt $.

Since $e(x) > 0$ for all $x$, for $x > 0$, from $e(x) =1+\int_0^x e(t) dt $, we get sequentially, $e(x) > 1$, $e(x) > 1+x$, $e(x) > 1+x+\frac{x^2}{2}$, so that, by induction, for any $n \ge 0$, $e(x) \gt \sum_{k=0}^n \frac{x^k}{k!} $.

For an upper bound on $e(x)$, assume that $0 < x < 1$ (since there is no polynomial bound for all $x$).

Let $f(x) = e(x)(1-x)$. $f(0) = 1$. $f'(x) =e'(x)(1-x)-e(x) =e(x)(1-x)-e(x) =-xe(x) < 0 $ so $f(x)$ is decreasing for $x > 0$. Therefore $f(x) < f(0) = 1$, so $e(x) < \frac1{1-x}$.

To get a linear bound on $e(x)$, suppose that $0 < x < a < 1$. We want a $c > 1$ such that $\frac1{1-x} \le 1+cx $ for $0 < x \le a$.

This is $1 \le (1-x)(1+cx) =1+x(c-1)-cx^2 $ or $cx \le c-1$ or $c(1-x) \ge 1$ or $c \ge \frac1{1-x} $.

Since $x \le a$, $\frac1{1-x} \le \frac1{1-a} $, so $c =\frac1{1-a} $ works.

Therefore $e(x) \le 1+\frac{x}{1-a} $ for $0 < x < a < 1$.

I'll leave it at this.