0

I have been trying to solve these but have had no success. Please help by giving hints not answers.

None

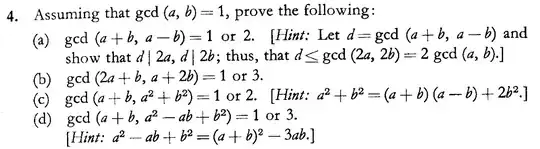
Assuming that $\gcd(a,b)=1$ prove the following:
(a) $\gcd(a+b,a-b)=1$ or $2$. [Hint: Let $d=\gcd(a+b,a-b)$ and show that $d\mid 2a$, $d\mid 2b$; thus $d\le \gcd(2a,2b) = 2\gcd(a,b)$]
(b) $\gcd(2a+b,a+2b)=1$ or $3$.
(c) $\gcd(a+b,a^2+b^2)=1$ or $2$. [Hint: $a^2+b^2=(a+b)(a-b)+2b^2$.]
(d) $\gcd(a+b,a^2-ab+b^2)=1$ or $3$. [Hint: $a^2-ab+b^2=(a+b)^2-3ab$]

Source: Elementary Number Theory by David M. Burton

Martin Sleziak
  • 53,687
TheRandomGuy
  • 4,014
  • 2
  • 20
  • 56
  • What is the question? it seems like you forgot to upload it... – Galc127 Feb 29 '16 at 06:17
  • It is difficult to give hints, not answers, since the supplied hints are close to what one might have given. But for Question (b), note that if $d$ divides both then $d$ divides $2(2a+b)-(a+2b)$, that is, $d$ divides $3a$. Similarly, $d$ divides $3b$. – André Nicolas Feb 29 '16 at 06:27
  • Please, post only one question in one post. Posting several questions in the same post is discouraged and such questions may be put on hold, see meta. It is also good to add the source of the question. – Martin Sleziak Feb 29 '16 at 07:25
  • BTW if you search a bit, you will find out that many of these questions have already been asked and answered on this site. The first one is here: http://math.stackexchange.com/questions/32737/prove-gcdab-a-b-1-or-gcdab-a-b-2-if-gcda-b-1 and http://math.stackexchange.com/questions/457296/prove-that-if-a-and-b-are-relatively-prime-then-gcdab-a-b-1-or-2 – Martin Sleziak Feb 29 '16 at 07:27
  • 3
    The main tool you will need to use is this: you can add any multiple of one number to the other number and the greatest common divisor won't change. In other words, $\gcd(a,b)=\gcd(a,b+ka)$ for any integer $k$. (Do you know why this tool is true?) – Greg Martin Feb 29 '16 at 08:31
  • The thrid one can be found here: http://math.stackexchange.com/questions/153125/prove-gcdab-a2b2-is-1-or-2-if-gcda-b-1 and http://math.stackexchange.com/questions/307545/how-can-i-find-the-possible-values-that-gcdab-a2b2-can-take-if-gcda – Martin Sleziak Feb 29 '16 at 10:44
  • For (4) see http://math.stackexchange.com/questions/257392/if-gcda-b-1-then-gcdab-a2-abb2-1-or-3 and http://math.stackexchange.com/questions/1222967/let-k-ab-a2b2-ab-if-a-b-1-then-k-1-or-k-3 – Martin Sleziak Feb 29 '16 at 10:49
  • For (2) see: http://math.stackexchange.com/questions/649433/suppose-a-b-1-then-2ab-a2b-1-text-or-3 – Martin Sleziak Feb 29 '16 at 10:50
  • @MartinSleziak Thanks. – TheRandomGuy Feb 29 '16 at 12:56

1 Answers1

0

Let $u = a + b$ and $v = a - b$. Clearly $u$ and $v$ are both odd or both even. Express $a$ and $b$ in terms of $u$ and $v$.

$\gcd(m,n) = g$ if and only if g is the smallest positive integer that can be expressed as $\alpha m + \beta n = g$

So there exists integers $\alpha$ and $\beta$ such that $\alpha a + \beta b = 1$ Change that into an expression involving $u$ and $v$ and go from there.

Steven Alexis Gregory
  • 26,769