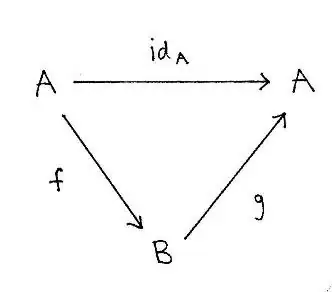
Theorem. Let $A$ and $B$ be sets. Consider the following three statements:
- $f\colon A\to B$ is one-to-one.
- There exists $g\colon B\to A$ such that $gf = \mathrm{id}_A$ ($f$ has a left inverse).
- For every set $C$ and every functions $h,k\colon C\to A$, if $fh = fk$ then $h=k$ ($f$ is left-cancellable).
Then 2$\implies$3$\iff$1. Moreover, if $A$ is nonempty, then 1$\implies$2 so all three are equivalent.
Proof.
2$\implies$3. Let $h,k\colon C\to A$ be such that $fh = fk$. Let $g$ be the function guaranteed by 2. Then
$$h = \mathrm{id}_Ah = (gf)h = g(fh) = g(fk) = (gf)k = \mathrm{id}_Ak = k.$$
Thus, $f$ is left-cancellable.
3$\implies$1. Let $a,a'\in A$ be such that $f(a)=f(a')$. We need to prove that $a=a'$. Let $C=\{0\}$, $h\colon C\to A$ be given by $h(0)=a$, and $k\colon C\to A$ be given by $k(0)=a'$. Then $fh(0) = f(a) = f(a') = fk(0)$. so $fh=fk$. Since $f$ is left-cancellable, we conclude that $h=k$. Hence $a = h(0) = k(0) = a'$, proving that $f$ is one-to-one.
1$\implies$3. Let $C$ be a set and $h,k\colon C\to A$ be such that $fh = fk$. We need to show that $h=k$. Let $c\in C$. Then $f(h(c)) = f(k(c))$; since $f$ is one-to-one, we conclude that $h(c)=k(c)$. Since $h(c)=k(c)$ for all $c\in C$, it follows that $h=k$.
1$\implies$2 if $A$ is nonempty and $B$ are nonempty. Since $A$ is nonempty, there exists $a_0\in A$. Define $g\colon B\to A$ as follows:
$$g(b) = \left\{\begin{array}{ll}
a &\text{if }b\in f(A)\text{ and }f(a)=b;\\
a_0&\text{if }b\notin f(A).
\end{array}\right.$$
This is well-defined, since $f(a)=f(a')=b$ implies $a=a'$. And if $b\in f(A)$, then there exists $a\in A$ such that $f(a)=b$. Now, let $a\in A$. Then $g(f(a)) = a$, so $gf = \mathrm{id}_A$, as desired. $\Box$
In particular, given a function $f\colon A\to B$, if a $g$ exists that makes the diagram commute, then $f$ is one-to-one. Conversely, if $f$ is one-to-one and $A$ is nonempty (or $A$ and $B$ are both empty), then we can find a $g$ that makes the diagram commute.
Here's the dual:
Theorem. Let $A$ and $B$ be sets. Consider the following three statements:
- $f\colon A\to B$ is onto.
- There exists $g\colon B\to A$ such that $fg=\mathrm{id}_B$ ($f$ has a right inverse).
- For every set $C$ and every functions $h,k\colon B\to C$, if $hf = kf$, then $h=k$ ($f$ is right-cancellable).
Then 2$\implies$3$\iff$1. Moreover, the implication 1$\implies$2 is equivalent to the Axiom of Choice.
Proof. 2$\implies$3 Let $C$ be a set and let $h,k\colon B\to C$ be such that $hf=kf$. Let $g$ be the function guaranteed by 2; then:
$$h = h\mathrm{id}_B = h(fg) = (hf)g =(kf)g = k(fg) = k\mathrm{id}_B = k.$$
3$\implies$1. Let $C=\{0,1\}$ and define $h\colon B\to C$ by $h(b)=1$ for all $b$, and
$$k(b) = \left\{\begin{array}{ll}
1 & \text{if }b\in f(A);\\
0 &\text{if }b\notin f(A).
\end{array}\right.$$
Then $hf = kf$, hence by 3 we have $h=k$. Therefore, $k(b)=1$ for all $b\in B$, hence $f(A)=B$; that is, $f$ is onto.
1$\implies$3. Suppose that $C$ is a set and $h,k\colon B\to C$ are functions such that $hf = kf$. Let $b\in B$; we need to show $h(b)=k(b)$. Since $f$ is onto, there exists $a\in A$ such that $f(a)=b$. Therefore,
$$h(b) = h(f(a)) = hf(a) = kf(a) = k(b).$$
Thus, $h=k$.
If the Axiom of Choice holds, then 1$\implies$2: If $f$ is onto, then for every $b\in B$, the set $f^{-1}(b) = \{a\in A\mid f(a)=b\}$ is nonempty. By the Axiom of choice, there exists a function $g\colon B\to \cup_{b\in B} f^{-1}(b)$ such that $g(b)\in f^{-1}(b)$ for each $b\in B$. I claim that $fg=\mathrm{id}_B$. Indeed, for every $b\in B$, $g(b)\in f^{-1}(b)$, so $f(g(b))=b$.
If 1$\implies$2 holds, then the Axiom of Choice holds. Let $\mathcal{X}=\{A_i\}_{i\in I}$ be a nonempty family ($I\neq\varnothing$) of nonempty sets ($A_i\neq\varnothing$ for each $I\in I$). We need to show that there exists a function $g\colon I\to\cup_{i\in I}A_i$ such that $g(i)\in A_i$ for each $i\in I$.
Let $B_i = A_i\times\{i\}$. Note that the family $\mathcal{Y}=\{B_i\}_{i\in I}$ consists of pairwise distinct sets. Let $Y=\cup_{i\in I}B_i$, an define $f\colon Y\to I$ by $f(b_i,i) = i$ (projection onto the second component). The map is onto, since each $A_i$ is nonempty, so $B_i\neq\varnothing$. By our assumption that 1$\implies$2, there exists $h\colon I\to Y$ such that $h(i)\in B_i$ for each $i\in I$. Let $\pi_i\colon B_i\to A_i$ be the projection onto the first coordinate, $\pi_i(b_i,i) = b_i$. Define $g\colon I\to \cup_{i\in I}A_i$ by
$$g(i) = \pi_i\circ h (i).$$
Since $h(i)\in B_i=A_i\times\{i\}$, then $\pi_i\circ h(i) \in A_i$. This holds for each $i$, so $g$ is the desired choice function. $\Box$
In particular, if the diagram commutes, then $g$ is onto. Conversely, assuming the axiom of choice, if $g$ is onto, then we can find an $f$ that fits into the diagram and makes it commute.