1

Notation: $\zeta(s) = \zeta(x+it)$

In http://dml.cz/bitstream/handle/10338.dmlcz/136881/MathSlov_53-2003-2_3.pdf the following inequality was proven:

$$ \left|\zeta\left(\frac 1 2 - d+it\right)\right| \ge \left| \zeta\left( \frac 1 2 + d + it \right) \right| \text{ for } 0\le d \le \frac 1 2 \text{ and } t \ge 2\pi+1. $$

Letting $d = 1/2$, we get:

$$ |\zeta(it) \ge |\zeta(1+it)|. $$

The question concerns the relation between $|\zeta(1+it)|$ and $|\zeta(x+it)|$ . Specifically, is the inequality below true:

$$ |\zeta(x+it)| \le |\zeta(1+it)| $$

The above inequality will complete the ordering of the three moduli as follows:

$$ |\zeta(x+it)| \le |\zeta(1+it)| \le |\zeta(it)| $$

Thank you for your support.

Michael Hardy
  • 1
Hass Saidane
  • 94
  • Thanks Michael for editing – Hass Saidane Feb 24 '16 at 16:25
  • @ hass : you know that the first inequality follows trivially from the functional equation $\zeta(s) = \chi(s) \zeta(1-s)$ ? – reuns Feb 24 '16 at 17:55
  • Thanks, but I didn't know and I don't know how it does.I'll appreciate an explanation how. Thanks – Hass Saidane Feb 24 '16 at 18:43
  • read https://en.wikipedia.org/wiki/Riemann_zeta_function#The_functional_equation and if you read french, the article in french is much better – reuns Feb 24 '16 at 18:46
  • I read both versions of the article which assert that: Modulus{Zeta(it)] = A(t) * Modulus[Zeta(1+it)] without explaining how this result was obtained. Also A(t) > 1 needs to be proven. In any case, the proof I provided is much easier. I am more interested in a proof of the second inequality. Any thoughts about it would be very helpful. Thanks again – Hass Saidane Feb 24 '16 at 20:19
  • Concerning the relation between the modulus of $\zeta(it)$ and $\zeta(1+it)$ see $(9)$ in this answer (from the real part of $(5)$). – Raymond Manzoni Feb 24 '16 at 23:21
  • Thanks Raymond for the reference. It's a great and direct approach to deal with the relation. The factor B(t) on the RHS of the answer needs to be greater than 1, to prove the relationship. Now what remains to prove is the second inequality. Any reference or idea about how to prove it will be very useful. Thanks again. – Hass Saidane Feb 25 '16 at 10:37
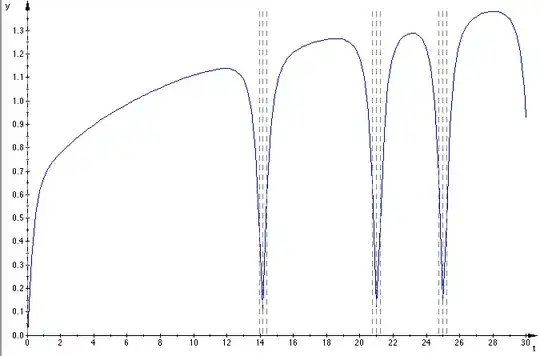  • Glad it helped @Hass Saidane (I should have added to divide $(6.1.30)$ and $(6.1.29)$ at page $256$ of A&S to conclude). Concerning $|\zeta(x+it)| \le |\zeta(1+it)|$ it doesn't appear right in general since $|\zeta(x+it)|$ will be as small as you wish near a zero of $\zeta$ compared to $|\zeta(1+it)|$ but the ratio becomes larger than $1$ between the zeros as illustrated in the linded picture of $;t\mapsto \left|\dfrac {\zeta(\sigma+it)}{\zeta(1+it)}\right|$ for $\sigma=\frac 12$ and $t\in[0,30]$. – Raymond Manzoni Feb 26 '16 at 00:09
  • (the symmetry around $\frac12$ of the inequality from the paper appears important!). Supposing $x>1$ doesn't look more promising. Sorry... – Raymond Manzoni Feb 26 '16 at 10:18
  • Thanks Raymond for the explanation. How about this inequality: Modulus[Zeta(x + it)] < Modulus[Zeta(it)]. It is supported by numerical results. Do you have an idea on how to prove it? – Hass Saidane Feb 26 '16 at 11:57
  • @Hass Saidane: you are right this one is much more promising but I didn't find a proof. In fact I would even conjecture something more precise for $x\in(0,1)$ : $$\left|\zeta(x+it)\right|\le\left(\frac {2,\pi}{t;\tanh\left(\frac{\pi}2,t\right)}\right)^{x/2}\left|\zeta(it)\right|$$ – Raymond Manzoni Feb 27 '16 at 01:32
  • Thanks Raymond. It's supported by numerical test results (see: http://dml.cz/bitstream/handle/10338.dmlcz/136881/MathSlov_53-2003-2_3.pdf , pg 150). Your conjecture is great. Is the factor A(t) < 1? A proof would be nice, even without the factor A(t). The only close reference I found was in Tichtmarsh's "The Zeta Function of Riemann", p.20: Zeta(x + it) = O(t^ (1/2- x/2) logt) for 0 <= x <= 1. At x = 0, we get: Zeta(it) = O(t^ 1/2)logt) so that: Modulus[Zeta(x + it)] < Modulus[Zeta(it)]. Is this correct, general? Thanks again. – Hass Saidane Feb 27 '16 at 10:43
  • I fear that relations like $\zeta(it) = O(t^{1/2}\log t)$ or better ones in the French Wikipedia won't help much (because of the implicit arbitrary coefficient in $O()$). Perhaps that subtraction $\zeta(x+it)-\zeta(it)$ or quotient expansions could return the wished results... who knows? Good luck anyway, – Raymond Manzoni Feb 27 '16 at 14:04
  • Thank you very much you for your help Raymond. If you ever get a reference or a proof for your conjecture, please pass it on. Thanks again. – Hass Saidane Feb 27 '16 at 15:10
  • I am on Linkedin if you'd like to connect and prove the Riemann Hypothesis – Hass Saidane Feb 27 '16 at 17:07

0 Answers0