The function $f: [0,1] → \mathbb R $ satisfies the equation $$f (x) = f \left (\frac x2 \right ) + f \left (\frac x2 + \frac 12\right)$$ for every $x$ in $[0,1]$.
Can we assert that $f (x) = c (1-2x)$ for some real $c$ if:
a) $f$ twice continuously differentiable on $[0,1]$;
b) $f$ continuously differentiable on $[0,1]$;
c) $f$ continuous on [0,1]?
I do not know the answer, the solution to all points. Please help.
Here is a continuous counterexample.
Write $\lfloor x\rfloor$ for the floor of $x$, and $\{x\}:=x-\lfloor x\rfloor$ for the fractional part. Let $g:[0,1]\to \mathbb{R}$ be a continuous function satisfying $g(0)=g(1)$, and define $$ f(x)=\sum_{n\geq 1} \frac{(-1)^{\lfloor2^n x\rfloor}}{2^n} g(\{2^n x\}). $$ It is an exercise to check that $f$ is continuous. It can also be checked that $$ f\left(\frac{x}{2}\right)=\frac{g(x)}{2}+\frac{1}{2}f(x),\hspace{1cm}f\left(\frac{x}{2}+\frac{1}{2}\right)=-\frac{g(x)}{2}+\frac{1}{2}f(x), $$ so that $f$ satisfies the functional equation.
If $g(x)=c$ is constant, then $f(x)=c(2x-1)$. If we take $g(x)$ to be non-constant, we get a different $f$. I have included a plot of $f$ when $g(x)$ is the distance from $x$ to the nearest integer.
This is a partial answer that proves the result when $f$ is asumed continuously differentiable. Let $M$ be the maximum of $f'$ on $[0,1]$. Define $A=\{a\in[0,1]:f'(a)=M\}$. Since $$2f'(a)=f'\left(\frac{a}{2}\right)+f'\left(\frac{1+a}{2}\right)$$ We see immediatly that $$a\in A\Longrightarrow(\frac{a}{2}\in A)\quad\hbox{and}\quad (\frac{1+a}{2}\in A) $$ Now, $A$ is not empty, and if $\alpha$ is an element from $A$ then the preceding property implies that $$\forall\,n\ge 1, k\in\{0,\ldots,2^{n-1}\},\quad \frac{k+a}{2^n}\in A$$ Now, $A$ is closed and contains a dense subset of $[0,1]$ it must be All the interval $[0,1]$, i.e. $A=[0,1]$.
This proves that $f'$ is constant, so $f(x)= m x+ c$ for some constants $m$ and $c$. Replacing back in the functionsl equation we conclude that we must have $m+2c=0$, that is $f(x)= -2c x+ c$ as desired.
The case of just continous solutions to the functionl equation seems difficult. The example of Julian-Rosen is remarkable.
Here is a way to find Julian's example. This functional equation is very well behaved under the Fourier transform. Let $f$ be an integrable solution of the equation. For any integer $n$, let:
$$\hat{f} (n) := \int_0^1 f(x) e^{-2\pi inx} \ dx.$$
Then:
$$\hat{f} (n) = \int_0^1 f \left( \frac{x}{2}\right) e^{-2\pi inx} \ dx + \int_0^1 f \left( \frac{x+1}{2}\right) e^{-2\pi inx} \ dx \\ = 2\int_0^{\frac{1}{2}} f (u) e^{-2\pi in (2u)} \ dx + 2 \int_{\frac{1}{2}}^1 f (u) e^{-2\pi in (2u-1)} \ dx \\ = 2 \hat{f} (2n).$$
Necessarily, $\hat{f} (0) = 0$. To get continuous solutions, take any sequence $(a_{2k+1})_{k \in \mathbb{Z}}$ which is summable and defined on the odd integers. Then extend this sequence to the integers by $b_0 = 0$ and:
$$b_{2^n (2k+1)} := 2^{-n} a_{2k+1},$$
and put $f(x) := \sum_{n \in \mathbb{Z}} b_n e^{2 \pi i nx}$. Then $f$ is continuous (its Fourier coefficients are summable), and satisfies the functional equation. If you want real-valued solutions, take the imaginary or real part (or choose $a_{-k} = a_k$).
More generally, the Fourier transform is well-defined when the coefficients are square-integrable. So you can choose a sequence $(a_{2k+1})_{k \in \mathbb{Z}}$ whose square is summable, extend it in the same way to a sequence $(b_n)_{n \in \mathbb{Z}}$, which will still be square-summable, and take the inverse Fourier transform. For instance, with $a_{2k+1} = -i(2k+1)^{-1}$, you get $b_n = -\delta_{0n} i n^{-1}$, so a solution to the functional equation is:
$$f(x) = 2\sum_{n=1}^{+ \infty} \frac{\sin (2 \pi n x)}{n},$$
which, up to a multiplicative constant, is $1-2x$. If you try to make this function periodic, it will have a discontinuity at the integers (which is hidden here by the fact that we worked on $[0,1]$), which explain that the coefficients of the Fourier transform are not summable.
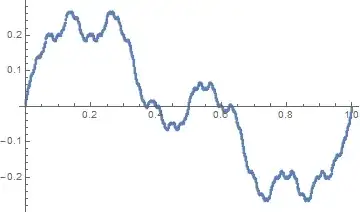
It can be shown that any continuous solution $f$ to the functional equation such that $f(0) = f(1)$ must at best have a modulus of continuity $\omega_f (h) \simeq h |\ln (h)|$ (and I think that this modulus of continuity is optimal almost everywhere), so they cannot be $\mathcal{C}^1$, and they look indeed pathological. This is because their Fourier coefficients do not decay very quickly.
With this method, you can solve other similar functional equations, say, for instance,
$$f(x) = \frac{2}{3} \left[ f \left( \frac{x}{2}\right) + f \left( \frac{x+1}{2}\right) \right],$$
or:
$$f(x) = f \left( \frac{x}{3}\right) + f \left( \frac{x+1}{3}\right) + f \left( \frac{x+2}{3}\right),$$
as well as some similar functional equations with more variables.
