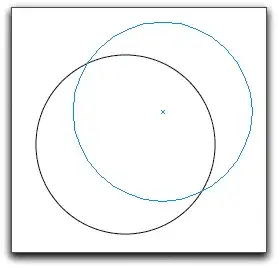
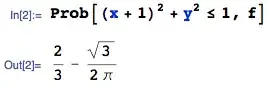If you would put a rabbit randomly on a circular table with radius $r= 1$ meter and it moves $1$ meter in a random direction, what is the chance it won't fall off?
I tried to do this using integrals, but then I noticed you need a double integral or something and since I'm in the 5th form I don't know how that works.
If the rabbit is placed at distance $x>0$ from the center, and moves straightforward in an uniformly distributed direction, his chances of not falling off are $$p(x)={2\arccos{x\over2}\over 2\pi}\ .$$ Assuming that his starting point is uniformly distributed with respect to area the probability $P$ that he will not fall of is therefore given by $$P={1\over\pi}\int_0^1 p(x)\cdot 2\pi x\>dx={2\over\pi}\int_0^1\arccos{x\over2}\>x\>dx\ .$$ Substituting $x:=2\cos t$ and partial integration then produce $$P={2\over3}-{\sqrt{3}\over 2\pi}\doteq0.391\ .$$
Hint: this problem is angularly symmetric. Therefore, only the starting distance from the center matters.
Consider a disk of radius $1$ centered at the origin. For a rabbit at $(x,0)$, for which angles does it fall off the table (do a little trig)? Now, use the symmetry and integrate.
To avoid the double integral, you can integrate along the positive radius and multiply each value you get by $2\pi r$ (the circumference of the circle with that radius). (This $2\pi r$ also comes out of the double integral because it's angularly symmetric.)
Let Roger Rabbit's location on the circular table be defined by the point $(X,Y)$, where random variables $X$ and $Y$ have a bivariate Uniform distribution inside the unit circle, with joint pdf $f(x,y)$:
By symmetry, we can assume, without loss of generality, that the rabbit jumps say 1m to the east (as Steve Jessop has noted above). Then, the probability that Roger Rabbit still lands on the table is $P[(X+1)^2 + Y^2 \leq 1]$:
All done.
Notes
Prob function used above is from the mathStatica package for Mathematica. As disclosure, I should add that I am one of the authors.