1

The goal of this question is to introduce basic group theory concepts with GAP: examples about alternating groups, cyclic groups and demonstrate the Lagrange theorem $[G:H]=\frac{\#G}{\# H}$.

Example.

I was surprised to find out that the number of elements in Klein four group, alternating group $A_4$ is 12, not 4,

enter image description here

which is equivalent to Elements(AlternatingGroup(4)) in GAP.

I would be extremely delighted to find GAP commands such as

  • command to print cosets ( CosetTable(AlternatingGroup(4)) firing error) and

  • command to find subgroups of A4.

which I want to use for more accessible demonstration for the Lagrange theorem in group theory. So

How to demonstrate Lagrange theorem with different introductory groups in GAP?

Community
  • 1
hhh
  • 5,469
  • 1
    I am confused: Klein 4-group has 4 elements, not 12, while $A_4$ has 12 elements indeed. – Olexandr Konovalov Feb 22 '16 at 00:47
  • @AlexanderKonovalov Thank you for the notice, I have clearly misunderstood the wiki hence even more important to demonstrate Klein four group and other introductory groups in GAP -- back to rereading the article: Klein four group of A4 is different thing to Klein four group? Have to verify things in GAP... – hhh Feb 22 '16 at 00:50
  • 1
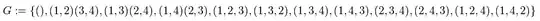
    OK. Please see 7.7: How do I get the subgroups of my group? about subgroups. As for cosets, look at RightCosets in the manual. CosetTable has another purpose, and has 2 arguments as documented. You should be suspecting that calling it with one argument is counterintuitive, becase cosets depend both on the group and on its particular subgroup, not just on the group. – Olexandr Konovalov Feb 22 '16 at 00:52
  • @ahulpke Thank you for your comment. I am aware of that question: this question is about demonstrating the Lagrange theorem, not about calculating subgroups (for which I show a command in GAP in the example). – hhh Feb 22 '16 at 15:13
  • 1
    G:=AlternatingGroup(4);D:=DerivedSubgroup(G);, now Size(G)/Size(D); is an integer - this is a demonstration. What else would you like to verify? It could make a good question if you ask to demonstrate with GAP hat the converse is not true: if $n$ divides $|G|$, it is not necessary that $G$ has a subgroup of order $n$. – Olexandr Konovalov Feb 23 '16 at 09:23
  • @AlexanderKonovalov like this? http://math.stackexchange.com/questions/1669123/if-h-divides-g-not-necessary-that-g-has-a-subgroup-of-order-h ? – hhh Feb 23 '16 at 19:52
  • hmm, I find formulations "special situation with Lagrange Theorem" and "How can you demonstrate the converse" confusing... – Olexandr Konovalov Feb 23 '16 at 20:40
  • @AlexanderKonovalov roger, updated :) – hhh Feb 23 '16 at 21:03

0 Answers0