Calculation of $\min$ distance between $x^2+y^2=9$ and $2x^2+10y^2+6xy=1$
$\bf{My\; Try::}$ Using the fact that the distance between two curve is independent of shifting.
So put $x=u+v$ and $y=u-v$ in thsese two curves, We get $\displaystyle u^2+v^2=\frac{9}{2}$
and $\displaystyle 2(u^2+v^2-2uv)+10(u^2+v^2-2uv)+6(u^2-v^2) = 1\Rightarrow 18u^2+6v^2-20uv=1$
But here again i get terms of $uv,$ So i did not understand how can i solve it,
Help me, Thanks
The original ellipse is congruent with the ellipse whose equation is $x^2+11y^2=1$. And all the ellipse which is similar to it has the equation form:$x^2+11y^2=\lambda$ Make it and $x^2+y^2=9$ as a equation group and solve it: $ x = \sqrt \frac{99-\lambda}{10} or -\sqrt \frac{99-\lambda}{10}, y = \sqrt \frac{\lambda -9}{10} or - \sqrt \frac{\lambda -9}{10}$.That means when $ 9<=\lambda <= 99$, the ellipse has intersection points with circle.
Therefore, when $\lambda = 9$ the ellipse tangent with the circle.
The words are so abstract possibly. 
Therefore the minimal distance becomes distance between the long axis vertexes. Since one of the long vertexes of $x^2+11y^2=1$ is (-1,0) and one of the long vertexes of $x^2+11y^2=9$ is (-3,0).
Hence, the answer should be 2.
Complement: 1) why elipse: $x^2+11y^2=1$ is congruent with elipse:$2x^2+10y^2+6xy=1$.
Designate $2x^2+10y^2+6xy=1$ as ellipse II. Designate $x^2+11y^2=1$ as ellipse I.
Think one of point$(x,y)$ on the ellipse II. Make it rotate about original point$(0,0)$ and it should fall into the ellipse $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $. Find the rotation matrix: $M = \left(\begin{matrix}cos(\theta)&-sin(\theta)\\sin(\theta)&cos(\theta)\end{matrix}\right)$ where $tan(\theta) = \frac{1}{3}$. Using rotation matrix multiply the column matrix $ \left(\begin{matrix}x\\y\end{matrix}\right)$every point(x,y) on the ellipse II can get every point(u,v) on the ellipse I. Now find the linear combination of $u^2, v^2$. Since $u^2 = f(x,y), v^2 = g(x,y)$ and the maximal degree of f(x,y) about x is 2. Similarly, the maximal degree of g(x,y) about x is 2. Through observing the coefficient, its equation should be $u^2 + 11 v ^2 = 1$.
2) Why choose $theta$ satisfying $tan(\theta) = \frac{1}{3}$? Because our target is to make the ellipse formalized. Luckily, the ellipse's reflecting point is $(0,0)$ because there is no monomial item(i.e. x y) in the original equation. Therefore, assume a line: $y = kx$ passing through the ellipse II. Make $ y=kx$ and $ 2x^2+10y^2+6xy=1$ as a equation group. Solve it. Get $ x = \sqrt \frac{1}{10k^2+6k+2} y = \sqrt \frac{k^2}{10k^2+6k+2} $ Since the long vertex point of the ellipse has maximal distance on the ellipse about $(0,0)$, just find the $ \max x^2+y^2$.
In a nutshell, the answer is 2.
If my answer has some errors or short points, please leave a comment.
Some hints:
The first curve $C_1$ is a circle centered at the origin, with radius $3$, and the second curve $C_2$ is a conic section of some sort.
To find the minimum distance between $C_1$ and $C_2$, you can just find the distance from $C_2$ to the origin, and then subtract $3$.
To find the distance from $C_2$ to the origin, you can minimize $x^2+ y^2$ subject to the constraint $2x^2 + 10y^2 + 6xy - 1 = 0$. In principle, this is a straightforward application of Lagrange multipliers. But in reality you may run into algebra problems, because finding the distance between a point and a conic section typically reduces to finding the roots of a polynomial of degree 4. This will be a huge mess of algebra unless the numbers have been chosen to give you an easy and obvious factorization.
Edit:
The comment from @Lab above is not quite correct, according to my calculations, but it's heading in a good direction. On the second curve $C_2$, have
$$
x = \frac{1}{\sqrt{10}} \left( 3\cos u + \frac{1}{\sqrt{11}}\sin u \right)
\quad ; \quad
y = \frac{1}{\sqrt{10}} \left( -\cos u + \frac{3}{\sqrt{11}}\sin u \right)
$$
So the distance (squared) to the origin is a quadratic function of $\sin u$ and $\cos u$. If you use the Weierstrass substitution
$$
\cos u = \frac{1-t^2}{1+t^2} \quad ; \quad
\sin u = \frac{2t}{1+t^2}
$$
you can convert this to a univariate rational function of $t$ of degree 4. You need to find the minimum value of this function. You could try finding the zeros of the first derivative algebraically, but this is likely to be very messy. Alternatively, use a numerical minimization procedure.
Edit #2:
Aha!! The ellipse is centered at the origin, which makes everything easy.
It's equation is
$$
(x,y) = \left(\frac{3}{\sqrt{10}}, \frac{-1}{\sqrt{10}}\right) \cos u +
\frac{1}{\sqrt{11}}\left(\frac{1}{\sqrt{10}}, \frac{3}{\sqrt{10}}\right) \sin u
$$
Note that the two vectors appearing in this equation are orthogonal unit vectors that give us the axes of symmetry of the ellipse. The lengths of the semi-major and semi-minor axes are $1$ and $1/\sqrt{11}$ respectively, so the ellipse lies entirely inside the circle.
The closest points to the circle are the ends of the major axis. The minimum distance is 2.
So, in the end, the key is to "diagonalize" the ellipse equation, which is just a simple eigenvalue problem. Further info on this topic in this question. The minimization techniques mentioned above are applicable in general, but are not needed here.
A hint:
The shortest segment connecting two points on the two different curves will meet both of them orthogonally. In particular it will meet the circle $x^2+y^2=9$ orthogonally, hence its prolongation will go through the origin. Therefore it is sufficient to find the points on the ellipse $2x^2+6xy+10y^2=1$ which are nearest to the origin
HINT...This is just a sketch of the method, which you might prefer to try for yourself.
You can find the directions of the axes of the ellipse by finding the eigenvectors of the matrix $$\left(\begin{matrix}2&3\\3&10\end{matrix}\right)$$
You will find that the minor semiaxis is along the line $y=3x$, and then it is a simple matter to find the difference between the length of this minor semiaxis and the radius of the circle, which will be the shortest distance you are looking for.
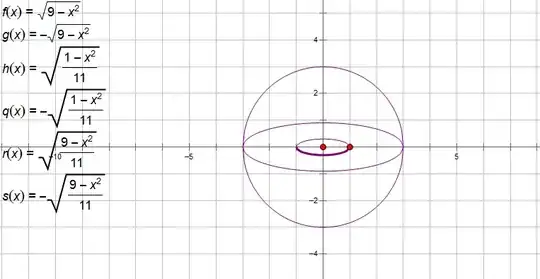
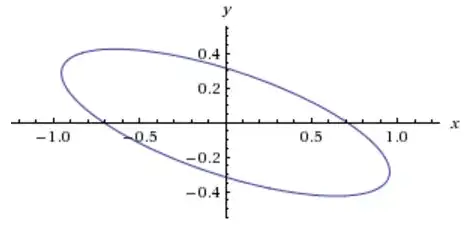
We have equation of a circle, x2+y2=9. Comparing with the standard equation of the circle (x−h)2+(y−k)2=r2 From the equation, the center of circle is (0,0) and radius is r=3. We have equation of the curve, g(x,y)=2x2+10y2+6xy=1 … (1) To find the center of the curve, we can find the normal to the curve. It is given by, ∇g(x,y)=0
⇒gx=0 and gy=0 We can partially (1) differentiate w.r.t x, we get, gx=4x+6y gx=0 ⇒4x+6y=0… (2) We can partially differentiate (1) w.r.t y, we get, gy=20y+6x gy=0
⇒20y+6x=0… (3) The point where the normal meet will be center of the curve. Solving (2) and (3), we get, Subtracting 4 times equation (3) from 6 times equation (2), we get 24x+36y=0−(24x+80y=0) 0x+116y=0¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ We get,y=0 . Now put this result in equation (1), we get x=0
(x,y)=(0,0)
Therefore, the center of the curve is also (0,0). From the figure we can understand that the distance between the circle and curve is radius of the circle minus the distance from origin to the curve. As the radius of the circle is constant, the required distance will be minimum when the distance from the curve to the origin is maximum. The distance from any point (x,y) on the curve to origin is given by, d=(x−0)2+(y−0)2−−−−−−−−−−−−−−−√=x2+y2−−−−−−√ ⇒d2=x2+y2
d is maximum when d2 is maximum. For maximizing, we use Lagrange multipliers. We need to maximize f(x,y)=x2+y2 over the constrain g(x,y)=2x2+10y2+6xy−1. By Lagrange multiplier, ∇f(x,y)=λ×∇g(x,y)
Taking partial derivative of f w.r.t x fx=2x Taking partial derivative of f w.r.t y fy=2y Taking partial derivative of g w.r.t x gx=4x+6y Taking partial derivative of g w.r.t y gy=20y+6x Applying Lagrange’s conditions, we get, fx=λgx2x=λ(4x+6y) On simplifying we get, ⇒x=λ(2x+3y)
⇒λ=x(2x+3y) … (4) fy=λgy2y=λ(20y+6x) On simplifying we get, ⇒y=λ(10y+3x) ⇒λ=y(10y+3x) … (5) On Comparing equations (4) and (5), we get, x(2x+3y)=y(10y+3x) On Cross multiplying, we get, (10y+3x)x=(2x+3y)y⇒10xy+3x2=2xy+3y2 On simplifying we get, ⇒3x2+8xy−3y2=0 Making complete square, (3–√x)2+2×(3–√x)×(43–√y)+(43–√y)2−(43–√y)2−3y2=0 ⇒(3–√x)2+2×(3–√x)×(43–√y)+(43–√y)2=163y2+3y2 ⇒(3–√x+43–√y)2=(16+93)y2=253y2
There is this beautiful property for curves that if you differentiate its equation w.r.t. $x$ (i.e., $y$ is constant) and similarly w.r.t. $y$ (i.e., $x$ is constant), then whatever lines or curves you get will intersect at the given curve's center.
In this case, differentiating w.r.t. $x$ gives $4x+6y=0$ and differentiating w.r.t. $y$ gives $20y+6x=0$. Clearly, they meet at the origin. Hence, the center of given curve is $(0,0)$.
So any point is of the form $(r\cos\theta,r\sin\theta)$ where $r$ is the distance from origin and $\theta$ is the angle with the $x$-axis.
Satisfying the curve's equation, we get, $r^2(6-4\cos2\theta+3\sin2\theta)=1$ Do it yourself you will get the same. $r^2=1/(6-4\cos2\theta+3\sin2\theta)$. For $r$ to be maximum, the denominator should be minimum.
$a\sin\Delta+b\cos\Delta$ always greater than equal to $-\sqrt{a^2+b^2}$ which in this case is= $-\sqrt{9+16} or $-5$.
$r^2$ max$=1/6-5=1$. $r$ max is $1$.
Hence radius of the circle is $3$ and r max for the curve is $1$. Both share a common center origin. So the minimum distance between them is $3-1=2$.
$2$ is the answer.
