Common tangent to two circles

Question

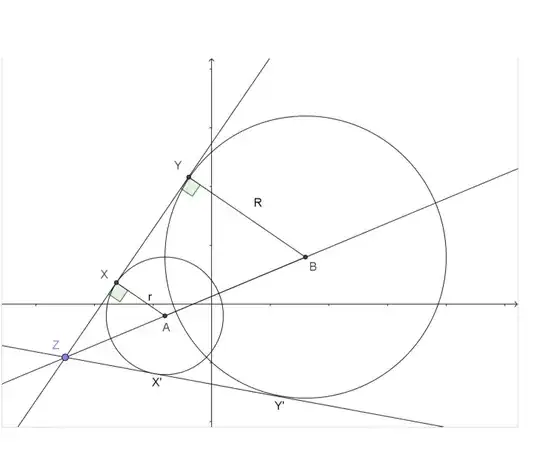
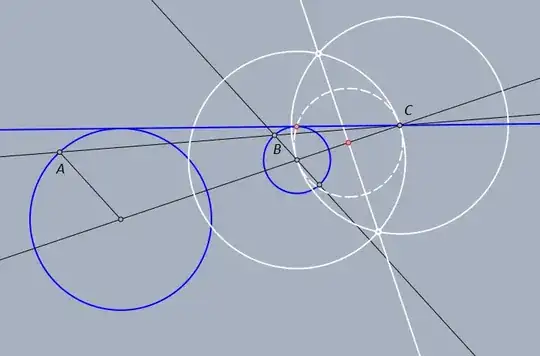
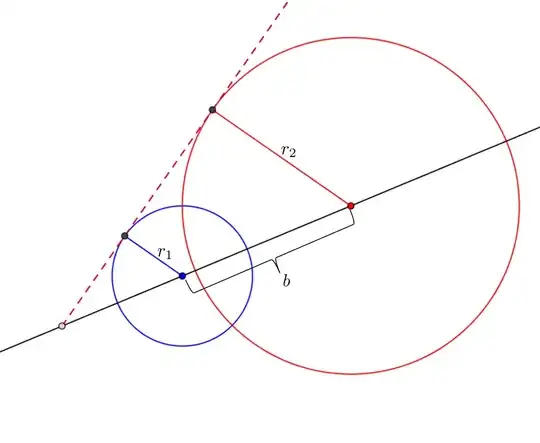
I need to find the common tangents to the following circles:

$~~~~~~~~\mathscr C_1:~x^2+y^2+8x+2y-8=0~~~~~$ and $~~~~~\mathscr C_2:~x^2+y^2-16x-8y-64=0$

How could I go about this? I found a similar question on the site but for some reason the person asking didn't want to use calculus, which lead to some lengthy solutions. Is there an easy way to do so with calculus?

Also, if someone were given one of the common tangents, together with the facts that:

• Both circles pass through $(-4,4)$
• Their centres lie on $12y=5x+8$

Would these three things alone be sufficient to determine the equations of $\mathscr C_1$ and $\mathscr C_2$?

Answer 1

For a non-elementary analytic geometry problem, lengthy and tedious solution should be expected and there are not too many short cuts, especially if the approach is non calculus.

1) From the equations $C_1$ and $C_2$, obtain the co-ordinates of centers and the radii.

2) Find $d = AB$, the distance between the centers.

3) The external common tangent will cut the line of centers at $Z$. Then, $t = ZA$ can be found by setting up ratios.

4) From the fact that $Z$ divides $AB$ externally in the ratio $t : (t + d)$, the co-ordinates of $Z(h, k)$ can be found.

This is the end of the easy part.

5) Let the required equation be $L: y = mx + c$; for some $m$ (we need to find out) but $c$ is governed by $h$ and $k$.

6) Setting the discrimant of $C_1$ and $L$ combined to $0$ to get the two values of $m$ (one for $ZXY$ and the other for $ZX’Y’$.

Another way to replace steps 5 and 6 is to use the formula that can give the equation of two common tangents from the external point $(h, k)$. It is too tedious to write, but is available through the internet.

Answer 2

A LATE ANSWER

I think there is an easier way to find the common tangent line than the one described in Mick's answer.

Of course the radii and the centers will have to be found first. Also, the equation of the line joining the centers will have to be found. But then...

Consider the following figure.

We have the two blue lines to which the common tangent has to be constructed.

• Take an arbitrary point on one of the circles. ($A$)
• Connect $A$ with the center of the respective circle.
• Draw a parallel to the latter line through the center of the other circle.
• This parallel will intersect the other circle. ($B$)
• Connect $A$ and $B$.
• The latter line will intersect the line joining the circle centers. ($C$)
• Halve $BC$ (red point)
• Draw a circle centered at the red point. (Broken white through $B$ and $C$.)
• This circle will intersect the (smaller) circle at the other red point.
• Connect $C$ with the "other red point." (blue line)
• The blue line will be tangent to both of the blue circles.

Answer 3

I think I have a simple solution using mostly algebra.

I assume you known how to extract the circle centers and the common line. Now measure the distance $b$ between the centers along the line, and note the circle radii, $r_1$ and $r_2$.

Now the tangents to a circle from a point A are found by drawing a new circle having the center and point A as the diametrical points. In order for the blue and red circles to have a common tangent, they must share common right triangles with the radii as the opposing sides and the diameters $d_1$ and $d_2$ as the hypotenuse. See below:

There are two equations given that are used to find the diameters $d_1$ and $d_2$

$$ \left. \begin{aligned} d_2 - d_2 &= b \\ \frac{r_1}{d_1} & = \frac{r_2}{d_2} \end{aligned} \right\} \Rightarrow \boxed{ \begin{aligned} d_1 & = \frac{b\, r_1}{r_2-r_1} \\ d_2 & = \frac{b\, r_2}{r_2-r_1} \end{aligned} } $$

Once $d_1$ is known then point A is specified along the common line. The tangent points are found by the intersection of the dotted blue and red circles and the solid blue and red circles. Algebraically, find the angle of the similar triangles with $$\sin \varphi = \frac{r_1}{d_1} = \frac{r_2}{d_2}$$. The use trigonometry to find the coordinates of $T_1$ and $T_2$.

That is with a coordinate system at A, and the x-axis along the common line move by $$T_1 = \pmatrix{d_1 - r_1 \sin \varphi \\ r_2 \cos \varphi}$$ and by $$T_2 = \pmatrix{d_2 - r_2 \sin\varphi \\ r_2 \cos\varphi}$$.