You stated that the center of the sphere is the origin of our 3-dimensional space, so suppose we have $O = (0, 0, 0)$, $Cam=(c_x, c_y, c_z)$ and $\overrightarrow{Dir}=\langle d_x, d_y, d_z \rangle$, and that the radius of the sphere is $R$.
Let $X = (r_x, r_y, r_z)$ be what we are solving for.
First, we need to find the plane containing both $Dir$ and $Cam$. Taking the cross product of $\overrightarrow{Dir}$ and $\overrightarrow{CamO}$, combined with the fact that the plane should contain $O = (0, 0, 0)$, the equation of our plane $P$ is $(c_zd_y - c_yd_z)x + (c_xd_z - c_zd_x)y + (c_yd_x - c_xd_y)z = 0$. We will later use this to ensure our point $X$ is on this plane.
Next, consider the conditions for $X$ to be the point at which $\overrightarrow{Hor}$ tangentially contacts the sphere. We need the point $X$ to be on the surface of the sphere, and we need the vectors $\overrightarrow{XO}$ and $\overrightarrow{XCam}$ to be perpendicular (in order for $\overrightarrow{XCam}$ to be tangent to the sphere).
For the first condition, we want $r_x^2 + r_y^2 + r_z^2 = R^2$, simply by substituting the coordinates of $X$ into the equation of our sphere.
For the second condition, we want $\overrightarrow{XO} \cdot \overrightarrow{XCam} = 0$. Since $\overrightarrow{XO} = \langle -r_x, -r_y, -r_z \rangle$ and $\overrightarrow{XCam} = \langle c_x - r_x, c_y - r_y, c_z - r_z \rangle$, we have $\overrightarrow{XO} \cdot \overrightarrow{XCam} = r_x^2 - c_xr_x + r_y^2 - c_yr_y + r_z^2 - c_zr_z = 0$. Note that we can simplify this equation by first substituting $r_x^2 + r_y^2 + r_z^2 = R^2$, and we obtain $c_xr_x + c_yr_y + c_zr_z = R^2$.
Thus, we now have a system of 3 equations and 3 unknowns:
- $(c_zd_y - c_yd_z)r_x + (c_xd_z - c_zd_x)r_y + (c_yd_x - c_xd_y)r_z = 0$
- $r_x^2 + r_y^2 + r_z^2 = R^2$
- $c_xr_x + c_yr_y + c_zr_z = R^2$
Now you can just pick your favorite way to solve it. This will give you the coordinates of $X$, and you will in turn have $\overrightarrow{Hor} = \overrightarrow{CamX}$. I haven't done the actual substitution yet as it's a huge mess, but I think this answers your question. I'm not exactly sure what you mean by the shortest calculation possible, but I think this method is straightforward and gives you a general expression for the coordinates of $X$ in terms of the parameters you provided.
Hope this helped.
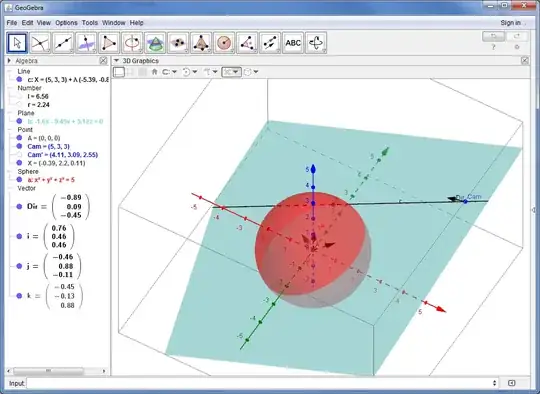
The resulting problem was much easier for me to solve.
– blackrack Feb 17 '16 at 03:13