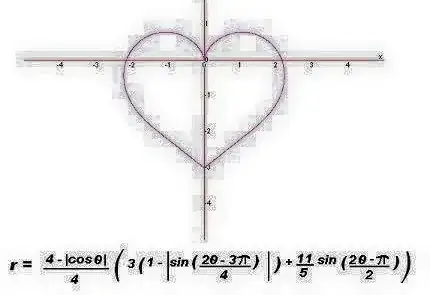
I came across this equation while surfing through the internet.Is this for real?If it is how is it done?
Asked
Active
Viewed 163 times
1
-
2There's always Batman http://math.stackexchange.com/questions/54506/is-this-batman-equation-for-real/152788#152788 :-). – copper.hat Feb 14 '16 at 08:21
-
1You can graph function y = f(x) on rectangular coordinates. Or you can graph the function $r = f(\theta)$ in polar coordinates where $\theta$ is an angle and $r$ is a distance from (0,0). This is a graph of such a function. – fleablood Feb 14 '16 at 08:21
-
To elaborate on @fleablood's comment: You can create shapes with a polar plot that you cannot do with the usual $x$-$y$ plot of a function. (And the other way around.) – copper.hat Feb 14 '16 at 08:27
-
There's no rule that you can only graph functions. if you graph $x^2 + y^2 = 1$ (or $r = 1$) get a circle and you can graph more than one thing. Anything drawable can be graphed although the trick is coming up with a simple formula for the graph. This heart one is one of the least surprising. THe nice thing about this heart is that it is a single function. Polar quardinates is nice for curves. $r = \theta$ is a spiral that would be hard (but possible) to express in rectangular coordinates – fleablood Feb 14 '16 at 16:58
1 Answers
2
Yes, it's real. You can try plotting it for yourself in Wolfram Alpha or some similar package. If your plotting package doesn't support polar coordinates, then you can convert to parametric equations in a rectangular coordinate system: $$ x(\theta) = r(\theta)\cos(\theta) \quad ; \quad y(\theta) = r(\theta)\sin(\theta) $$
There is even a well-known curve known as a cardioid, which is fairly similar to your heart-shaped one. If you have been the victim of a classical education, you will know that "cardio" means "related to the heart".
bubba
- 43,483
- 3
- 61
- 122
-
1
-
-
Just for fun. Some people would say that a classical education (including Latin and Greek and so on) is a pointless and painful ordeal. – bubba Feb 14 '16 at 12:49
-
-
-