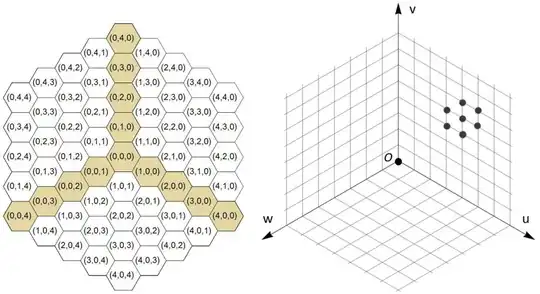
What if we used three axes on a plane like in the picture below? Then we could define any point on a plane using three numbers:
$$P=(a,b,c)$$
Three numbers seems excessive, however we do not need to use negative numbers that way.
$$a,b,c \geq 0$$
Of course, such coordinates in general will not be unique, since:
$$0=(0,0,0)=(1,1,1)=(2,2,2)=...$$
We can define a canonical form for each number this way:
$$m=\min(a,b,c)$$
$$P=(a,b,c)-(m,m,m)$$
This is not much different from using '$-$' sign in the usual complex plane.
The important point is that negative real numbers have the canonical form:
$$(-a,0,0)=(0,a,a)$$
On the left picture you can see how the numbers with integer coordinates form hexagonal cells. However, if we can use the easily scalable cells on the right side to define fractional coordinates.
The arithmetics is simple:
$$(a_1,a_2,a_3) \pm (b_1,b_2,b_3)=(a_1\pm b_1,a_2 \pm b_2,a_3 \pm b_3)$$
We can always get rid of any negatives by transforming the result to canonical form.
The multiplication law can only be defined as follows:
$$(a_1,a_2,a_3) \cdot (b_1,b_2,b_3)=(a_1 b_1 + a_2 b_3 + a_3 b_2, a_3 b_3+a_1 b_2+a_2 b_1,a_2 b_2 + a_1 b_3+a_3 b_1)$$
If we let $a$ be the real part of the number, then this rule agrees well with the rules for real numbers. It's also commutative, associative and transitive.
The conjugate of any number is defined:
$$P^*=(a,b,c)^*=(a,c,b)$$
Then we can see that multiplication by its conjugate gives the square of the norm:
$$||P||^2=(a,b,c) \cdot (a,c,b)=(a^2 + b^2+c^2, bc+ac+ab,bc + ab+ac)=$$
$$=(a^2 + b^2+c^2-bc-ac-ab,0,0)=a^2 + b^2+c^2-bc-ac-ab$$
The inverse of the number is introduced this way:
$$\frac{1}{P}=\frac{1}{(a,b,c)}=\frac{(a,c,b)}{a^2 + b^2+c^2-bc-ac-ab}$$
Finally let's introduce the units:
$$(a,b,c) = (a,0,0)+(0,b,0)+(0,0,c)=a+b \mathbb{j}+c \mathbb{k}$$
Using the multiplication law above we can show that:
$$\mathbb{j}^2=\mathbb{k}$$
$$\mathbb{k}^2=\mathbb{j}$$
$$\mathbb{j k}=\mathbb{k j}=1$$
These are just cube roots of unity:
$$\mathbb{j}^3=1$$
$$\mathbb{k}^3=1$$
The units are not linearly independent!
$$1+\mathbb{j}+\mathbb{k}=(1,1,1)=0$$
The imaginary unit will be:
$$\mathbb{i}=\frac{1}{\sqrt{3}}(\mathbb{j}-\mathbb{k})=\frac{1}{\sqrt{3}}(0,1,-1)=\frac{1}{\sqrt{3}}(1,2,0)$$
So this number field works as well as the complex number field,doesn't it? Why is it never introduced in textbooks? Isn't it useful, especially with its relation to the hexagonal coordinate system?