I was originally under the impression that a primal LP had a single corresponding dual feasible set. However, it is possible to alter the primal to an algebraically equivalent form which has a different dual feasible set than the unaltered version.
For example, suppose you're given:
$\text{minimize: } x_1+x_2 \\ \text{subject to: } x_1+x_2\geq3 \\~~~~~~~~~~~~~~~~2x_1+x_2\geq 4 \\~~~~~~~~~~~~~~~~x_1\geq 0, x_2\geq 0$
Then the dual is:
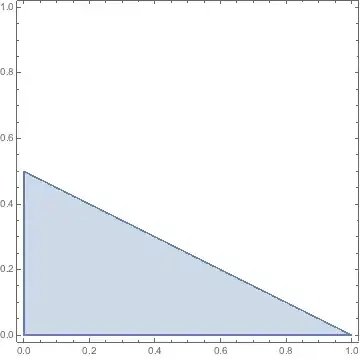
$\text{maximize: } 3\pi_1+4\pi_2 \\ \text{subject to: } \pi_1+2\pi_2\leq 1 \\~~~~~~~~~~~~~~~~\pi_1+\pi_2\leq 1 \\~~~~~~~~~~~~~~~~\pi_1\geq 0, \pi_2\geq 0$
which has the feasible set:
If you multiply the first primal feasible set inequality by 2 to get $2x_1+2x_2\geq 6$, the primal feasible set remains the same. However, the corresponding dual becomes
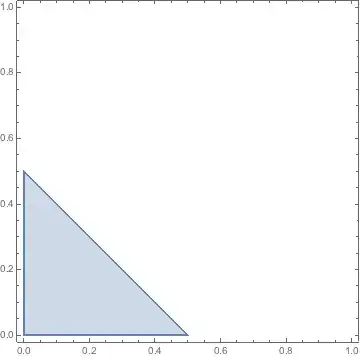
$\text{maximize: } 6\pi_1+4\pi_2 \\ \text{subject to: } 2\pi_1+2\pi_2\leq 1 \\~~~~~~~~~~~~~~~~2\pi_1+\pi_2\leq 1 \\~~~~~~~~~~~~~~~~\pi_1\geq 0, \pi_2\geq 0$
which has the feasible set:
Forgive the obviousness of this statement, but then the dual feasible set is not necessarily strictly related to the primal feasible set, but rather to the combination of the primal feasible set and the primal objective function.
Since it is possible to transform the dual feasible set, is there any preferable transformation which makes solving the LP easier? For instance, is there a transformation which reduces the number of vertices in the dual-feasible polytope?