10

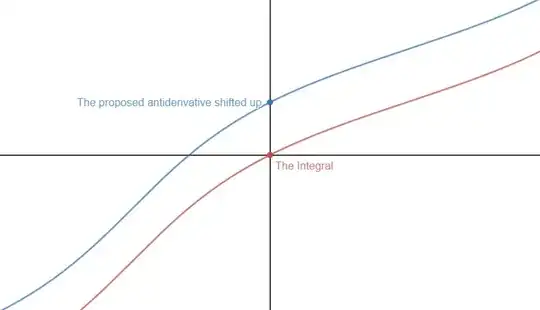
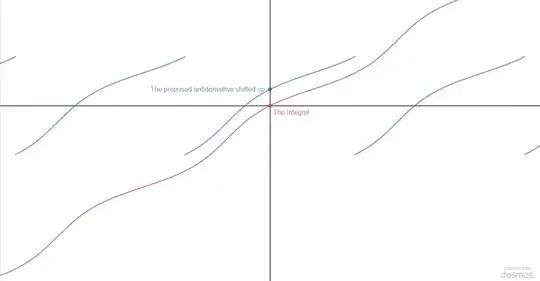
I use tangent half-angle substitution to calculate this indefinite integral: $$ \int \frac{1}{2+\sin x}\,dx = \frac{2}{\sqrt{3}}\tan^{-1}\frac{2\tan \frac{x}{2}+1}{\sqrt{3}}+\text{constant}. $$

Wolfram Alpha also give the same answer. However, $\frac{2}{\sqrt{3}}\tan^{-1}\frac{2\tan \frac{x}{2}+1}{\sqrt{3}}$ is discontinuous on $(n+1)\pi$ where $n$ is any integer. Why is an anti-derivative of a continuous function discontinuous?

egreg
  • 238,574
radi
  • 131
  • 4
  • 4
    The substitution is only valid on intervals of the form $(n\pi,(n+1)\pi)$. – egreg Feb 13 '16 at 16:43
  • We know the continuous function $x\mapsto\frac{1}{2+\sin x}$ ___will___ have an anti-derivative which is continuous (and even differentiable of course) everywhere. – Jeppe Stig Nielsen Feb 13 '16 at 16:46
  • 1
    The final integral has removable discounuous points. Once using limit to fix it, it is still continuous function. The discountinuous point is introduced by subsititution. – runaround Feb 13 '16 at 16:51
  • Why do you think this is genuinely discontinuous? Would you say the formula sin(x)/x is discontinuous at 0? It has a removable discontinuity there, so it easily extends to a continuous function at 0. Likewise, please try computing your formula at, say, $x = \pi$ and you'll see there is no problem! Your formula has removable discontinuities. – KCd Feb 13 '16 at 16:51
  • 2
    Another option is to find the primitive $$\frac{x}{\sqrt{3}}+\frac{2}{\sqrt{3}}\arctan\Bigl(\frac{\cos x}{2+\sqrt{3}+\sin x}\Bigr).$$ – mickep Feb 13 '16 at 16:54
  • 1
    @KCd Any valid anti-derivative (or primitive function) of this particular function must be strictly increasing (and injective for that reason). The resulting function as written in the question is $2\pi$-periodic which cannot be correct. – Jeppe Stig Nielsen Feb 13 '16 at 17:00
  • @JeppeStigNielsen : Might it be correct if one uses different "branches" of the "multiple-valued" arctangent function? $\qquad$ – Michael Hardy Feb 13 '16 at 17:03
  • Possible duplicate of A little integration paradox – J. M. ain't a mathematician Mar 05 '16 at 01:46

3 Answers3

2

Let's examine the first troublesome positive point, that is, $\pi$. We know that an antiderivative in the interval $(-\pi,\pi)$ is $$ f_0(x)=\frac{2}{\sqrt{3}}\arctan\frac{2\tan(x/2)+1}{\sqrt{3}}+c_0 $$ We also know that an antiderivative in the interval $(\pi,3\pi)$ is of the form $$ f_1(x)=\frac{2}{\sqrt{3}}\arctan\frac{2\tan(x/2)+1}{\sqrt{3}}+c_1 $$ Note that $$ \lim_{x\to\pi^{-}}f_0(x)=\frac{\pi}{\sqrt{3}}+c_0 $$ and $$ \lim_{x\to\pi^{+}}f_1(x)=-\frac{\pi}{\sqrt{3}}+c_1 $$ so in order to get continuity at $\pi$ we have $$ c_1=\frac{2\pi}{\sqrt{3}}+c_0 $$

Do the same for the other intervals.

egreg
  • 238,574
  • And note that while you wrote this answer, mickep gave a closed formula for a correct (on all of $(-\infty , \infty )$) indefinite integral. – Jeppe Stig Nielsen Feb 13 '16 at 17:07
  • @JeppeStigNielsen Nicely done! I'd also note that a similar problem happens with $\int|\sin x|,dx$. – egreg Feb 13 '16 at 17:10
1

One thing not emphasized much in the conventional calculus curriculum is that things like $$ \int \frac{dx} x = \log|x| + \text{“constant”} $$ are not true unless one takes “constant” to mean piecewise constant: $$ \int \frac{dx} x = \log|x| + \begin{cases} \text{one constant} & \text{if }x>0, \\ \text{another constant} & \text{if }x<0. \end{cases} $$ and: \begin{align} & \int \sec x\,dx \\[4pt] = {} & \log|\sec x+\tan x| + \cdots \text{what?} \\ & \cdots + \text{a different constant on each interval between vertical asymptotes.} \end{align} The comments under the question itself are pretty good so far:

  • “egreg” points out that the technique involving the tangent half-angle substitution is valid only on intervals between vertical asymptotes of the function $x\mapsto\tan\frac x 2$. That means it doesn't rule out anything that happens at those points: it doesn't say that there's an answer there or that there's not.
  • Jeppe Stig Nielsen points out that the antiderivative must be everywhere increasing since the function being integrated is everywhere positive. That means the answer cannot be a periodic function.
  • “runaround” and “KCd” remind us that there is such a thing as removable discontinuities.
  • You yourself point out that the antiderivative of a continuous function should be continuous.

Now just put all four of these points together and figure out which “piecewise constant” will give you a continuous function. That function will be everywhere increasing.

Michael Hardy
  • 1
0

We have the following definite integral:

$$f(x)=\color{#dd1111}{\int_0^x\frac{dt}{2+\sin(t)}}\stackrel?=\color{#4488dd}{\frac{2}{\sqrt{3}}\tan^{-1}\frac{2\tan \frac{x}{2}+1}{\sqrt{3}}}-\frac\pi{3\sqrt3}$$

At first, I wouldn't doubt this solution:

enter image description here

But then I look at the big picture:

enter image description here

It's not that the integral in question is discontinuous, it's that

a) the proposed solution is discontinuous for fixed constant.

b) a u-substitution was made that was not valid for $|x|\ge\pi$. To remove this problem, one could take $n=x\text{ mod }2\pi$ so that we make the argument between $(-\pi,\pi)$ and add in a linear piece of $n\int_{-\pi}^{\pi}\frac{dt}{2+\sin(t)}$.

Simply Beautiful Art
  • 74,685