1

The Ailles rectangle (named after an Ontario high school teacher, D. S. Ailles) is a rectangle of size $\sqrt{3}\times\sqrt{3}+1$ with three kind of triangles, like below.

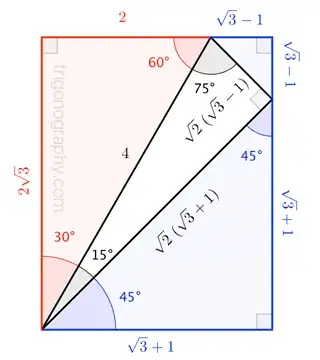
enter image description here

enter image description here

We have triangle 90-30-60 at the ceneter in the first rectangle, and 90-45-45 in the second. It is easy to compute exact values of e.g. $\sin{^\circ15}$. What values of angles and lengths of sides would have third rectangle with 90-15-75 triangle in the center? enter image description here

Blue
  • 75,673
TheKwiatek666
  • 479
  • The inner triangle can't be uniquely determined just by specifying the angles. You can think of sliding the point on the base sliding, and each such point defines a triangle. Therefore, I assume the additional condition that the point on the base divides base into sides of $\sqrt 3$ and $1$ (as in previous examples) is required to uniquely define the triangle. – taninamdar Feb 11 '16 at 22:46
  • @taninamdar I disagree. If you slide the point along the bottom of the rectangle, you can't keep the inner triangle $15$–$75$–$90$. – David Feb 12 '16 at 05:19
  • Note that these are special cases of my Angle-Addition trigonographs, shown in this answer. There are actually two candidates for Aille rectangles with a central $15^\circ$-$75^\circ$-$90^\circ$ triangle: (1) $\alpha = 45^\circ$ and $\beta= 15^\circ$; (2) $\alpha = 30^\circ$ and $\beta = 15^\circ$. The corresponding rectangle dimensions are (proportional to) (1) $(2\sqrt{3})\times(\sqrt{3}+1)$ and (2) $4\times(3+\sqrt{3})$. – Blue Feb 12 '16 at 05:41
  • FYI: The Ailles rectangle is a jumping-off point for a paper by Jack Calcut with the deceptively-simple title, "Grade School Triangles". – Blue Feb 12 '16 at 07:10

2 Answers2

1

Note. I answered the question on the assumption that the rectangle had to be $\sqrt{3} \times (\sqrt{3}+1)$ as in the third figure above. But Blue's answer shows that that may not be what the OP really needs.

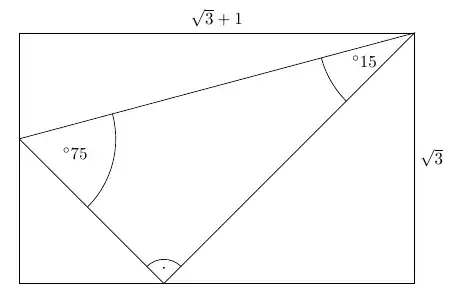
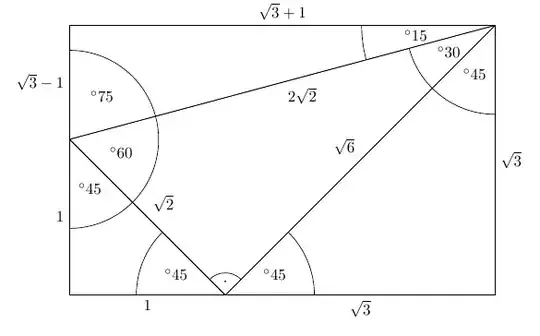
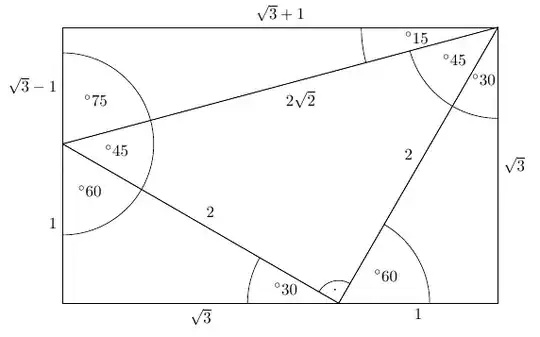
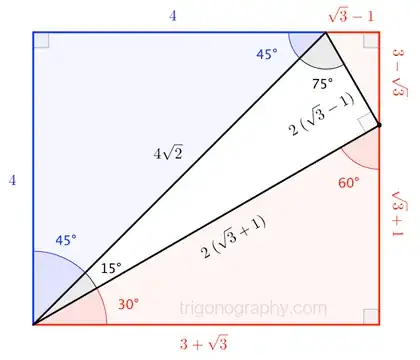
Call the inner triangle I, the bottom right triangle II, the bottom left triangle III and the upper triangle IV.

The first thing to note is that triangles II and III are similar. Since the ratio of their hypotenuses is $\tan 15^{\circ}$, we deduce that the bottom of triangle III has length $\sqrt{3} \tan 15^{\circ} = 2\sqrt{3} - 3$. From this, we find that the remaining leg of triangle I is $4-\sqrt{3}$. Using the similarity of II and III again, the other leg of III is $11-6\sqrt{3}$. The missing leg of IV is then $7\sqrt{3} - 11$.

The Pythagorean theorem can be used to find the sides of the inner triangle. All the sides have roots inside roots and cannot be simplified further.

The upper angle of triangle II is $\arctan(4/\sqrt{3}-1)$, which Wolfram Alpha is unable to simplify.

David
  • 6,306
1

Here are two candidate diagrams (I think I prefer the second) based on my Angle-Addition trigonographs.

enter image description here

enter image description here

Note: If we name the angles in the bottom-left corner in counter-clockwise order as $\alpha$, $\beta$, $\gamma$ (in the OP's diagrams, these are in the top-right corner in clockwise order), then the (width-to-height) aspect ratio of the rectangle in such a trigonograph is $\cos\alpha\cos\beta : \cos\gamma$. The original Ailles rectangles are similar because they exchange $\alpha$ and $\beta$.

Blue
  • 75,673
  • The OP required the rectangle to be $\sqrt{3} \times (\sqrt{3} + 1)$. I understand that you are saying these rectangles serve the same purpose as the first two Ailles' triangles in that they allow you to find the trigonometric functions of $15^{\circ}$. Is that correct? – David Feb 12 '16 at 06:45
  • I didn't read the $\sqrt{3}\times(\sqrt{3}+1)$ ratio as a requirement, per se, so yes: I'm offering diagrams in the spirit of the originals, handy mnemonic devices for the trig ratios of $15^\circ$, $30^\circ$, $45^\circ$, $60^\circ$, and $75^\circ$. You can consider this answer an illustrated elaboration on my comment below the question. :) – Blue Feb 12 '16 at 06:59