Can a complex argument into this function ever yield a real result?

Question

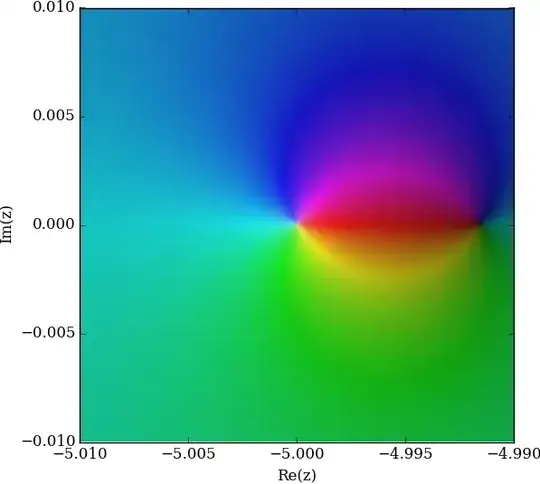
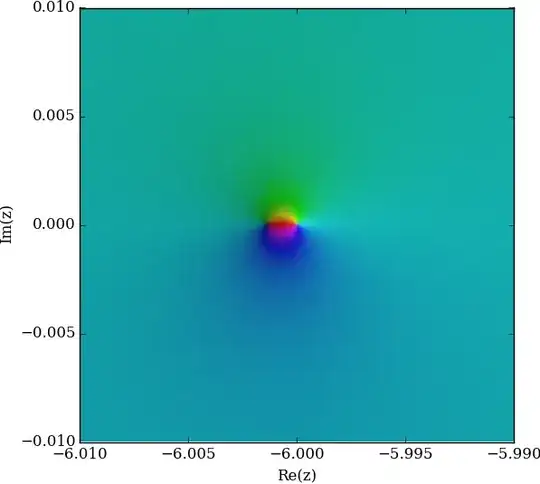
I have a function defined as:

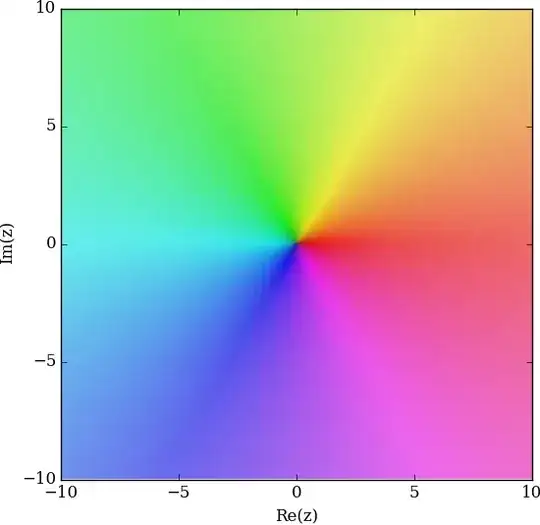
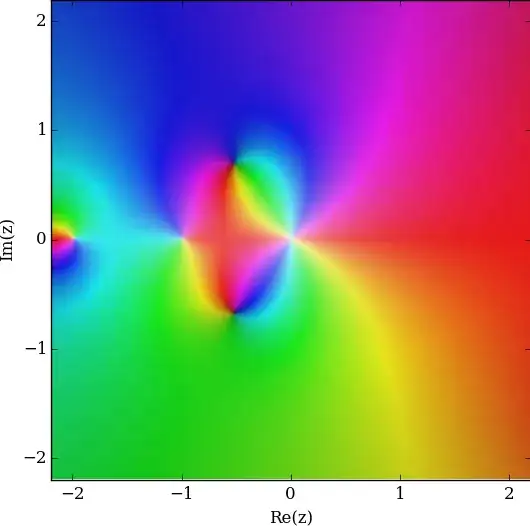
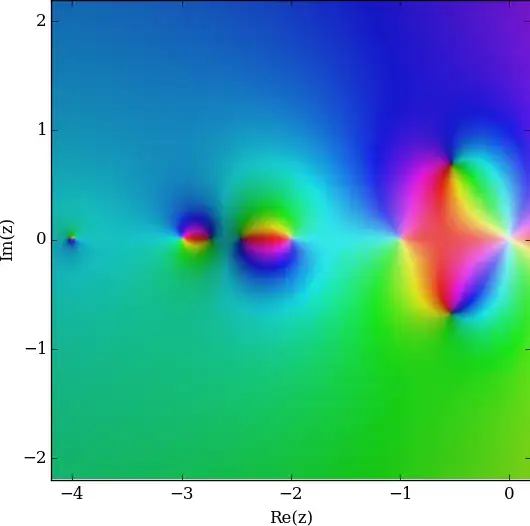
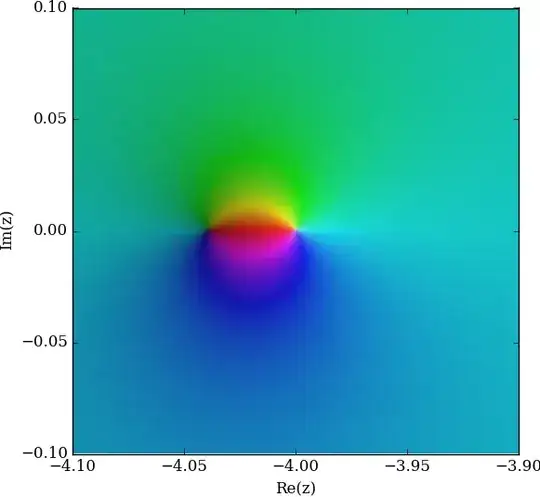
$f(z)=\frac{\Gamma{(z)}+1}{z}$

Are there any $z ∈ C$ (with nonzero imaginary part) such that $f(z)∈R$?

I tried substituting in $z=a+bi$ with $b≠0$ into the product and integral definitions of the Gamma function, but with little effect.

EDIT:

$f(z)=\frac{\Gamma{(z)}+1}{z}$

$f(a+bi)=\frac{\Gamma(a+bi)}{a+bi}+\frac{1}{a+bi}$

Introduce the variable $R$, denoting a real number. Then let $R=f(a+bi)$:

$R=\frac{\Gamma(a+bi)}{a+bi}+\frac{a-bi}{a^2+b^2}$

By definition $\Im(R)=0$. Re-arranging we get:

$R-\frac{a}{a^2+b^2}+\frac{b}{a^2+b^2}·i=\frac{\Gamma(a+bi)}{a+bi}$

Because $R$ can be any real number, the 'real' part of the equation may always be true for some R. Therefore, equating the $\Im$ parts of each side of the equation, we get:

$\frac{b}{b^2+a^2}=\Im(\frac{(a-bi)\Gamma(a+bi)}{a^2+b^2})$

Because $a,b$ are strictly real numbers, $a^2+b^2$ must be real and the same on both sides.

Therefore,

$b=\Im((a-bi)\Gamma(a+bi))$

$b=\Im((a\Gamma(a+bi)-bi\Gamma(a+bi))$

$b=a\Im(\Gamma(a+bi))-b\Re(\Gamma(a+bi))$

It follows that:

$\frac{b}{a}=\frac{\Im(\Gamma(a+bi))}{1+\Re(\Gamma(a+bi))}$

Adding 1 to both sides:

$\frac{b}{a}+1=\frac{\Im(\Gamma(a+bi))}{1+\Re(\Gamma(a+bi))}+\frac{1+\Re(\Gamma(a+bi))}{1+\Re(\Gamma(a+bi))}$

$\frac{b}{a}+1=\frac{\Gamma(a+bi)+1}{1+\Re(\Gamma(a+bi))}$

EDIT II It turns out I may have proceeded incorrectly in the last step. You see, the last equation re-arranges to:

$\frac{z}{\Re(z)} = \frac{\Gamma(z)+1}{1+\Re(\Gamma(z))}$

And consequently:

$\frac{1+\Re(\Gamma(a+bi))}{\Re(z)} = \frac{\Gamma(z)+1}{z}$, which is the normal, real number solution. (i.e. $b=0$).

If we go back a few steps and instead eliminate the real part, we get the following:

$\frac{b}{a}=\frac{\Im(\Gamma(a+bi))}{1+\Re(\Gamma(a+bi))}$

$\frac{a}{b}=\frac{1+\Re(\Gamma(a+bi))}{\Im(\Gamma(a+bi))}$

Now, adding 1, we get:

$\frac{a}{b}+1=\frac{1+\Re(\Gamma(a+bi))+\Im(\Gamma(a+bi))}{\Im(\Gamma(a+bi))}$

$\frac{z}{\Im(z)}=\frac{1+\Gamma(z)}{\Im(\Gamma(z))}$

Therefore, if $z=a+bi$ with $b≠0$ then the only time when $f(z)$ can be real is when:

$f(z)=\frac{\Im(\Gamma(z))}{\Im(z)}$

Answer 1

The derivative of $f$ vanishes at many points on the real axis (at least once between every consecutive negative integers, just by looking at the limits there)

On some small enough complex neghbourhoods of those points, $f$ is then at least $2$-to-$1$, which means that there are complex inputs to $f$ that give real outputs.

Answer 2

I will provide a heuristic method to conclude that yes, such values exist, using a domain coloring visual argument. A domain coloring applies a color to each point in the complex plane based solely on its polar angle --- i.e. write $a+bi=Re^{i\theta}$ and we assign the colors based on $\theta$ (the $R$ decides brightness, typically).

If I apply the (Python, mpmath) domain coloring algorithm to the identity function $f(z)=z$ I get the following image:

.

The important thing about this image is that you notice the positive $x$-axis is colored red --- clockwise from red we move towards yellow and counterclockwise from red we get magenta. If we were to continuously go from magenta towards yellow in a clockwise direction, we must pass through the reddish area (the center of which colors the positive real numbers).

Now I will apply a domain coloring to your function $f(z)=\dfrac{\Gamma(z)+1}{z}$:

Notice in this image there are many "fingerlike" structures on the right. As Joanpemo noted, many values where $z \in \mathbb{R}$ yield real values (and hence are colored red in the image). Where else could $f$ be real?

Since $f$ is the sum and quotient of functions continuous on $\mathbb{C} \setminus \{0,-1,-2,\ldots\}$, we know that the function $f$ is continuous near the fingerlike structures and our image shows magenta --> red --> yellow color transitions (i.e. argument transitions from negative to positive) of $f(z)$ near the fingerlike structures.

It also appears that there is a sequence of strange areas going left along the $x$-axis near each nonpositive integer. These structures come from the fact that $\Gamma$ has poles at such points. Here's some zoomed in images of those places:

To make these images just change XMIN, XMAX, et al to desired values:

#!/usr/bin/python
import numpy as np
import matplotlib.pyplot as plt
from mpmath import *

cplot(lambda x: (gamma(x)+1)/x,[XMIN,XMAX],[YMIN,YMAX],points=50000,verbose=True)
plt.savefig('FILENAME.png')

Answer 3

$$\forall\,n\in\Bbb N\;,\;\;\Gamma(n)=(n-1)!\implies f(n)=\frac{(n-1)!+1}n\in\Bbb Q\subset\Bbb R$$