Proving that the Calkin-Wilf tree enumerates the rationals.

Question

The Calkin-Wilf tree is an infinite undirected graph (tree) which is constructed as follows: starting from the root at $\frac{1}{1}$, each node $\frac{a}{b}$ has two children:

• a left child $\frac{a}{a+b}$
• a right child $\frac{a+b}{b}$

This tree has the property that every rational appears in it exactly once, in lowest terms. I'm interested in ways to intuitively understand this fact.

Most of what I know on this topic comes from this wonderful blog, which gives a proof [*] of the above at the link. He points out that every child uniquely defines a parent, and that every parent has a either a smaller numerator or a smaller denominator than its child. Therefore, if you start from any fraction $\frac{p}{q}$ in lowest terms, you can always trace a path back to $\frac{1}{1}$, the root.

This is a really nice proof, but it feels a bit "backwards" to me, in that we visualize walking the tree from the bottom up. Does anyone know of alternate proofs of this fact? I don't need rigor, just intuition.

Thoughts:

Clearly, all children must have either a greater numerator or a greater denominator than any of their ancestors, so they can't be repeats of an ancestor. (We also need "lowest terms" for this, but that follows by a separate argument -- see footnote).

So I'm only worried about "cousins". Perhaps there is some property that all the left children of a node share, which the right children do not? That would solve the problem, I believe.

_{*My summary only covers the part of his argument that proves "every rational appears in it exactly once." The "in lowest terms" part involves Euclid's Algorithm, and is covered in the next post.}

Answer 1

Let's use a binary encoding for our way from the top of the tree to a particular fraction. We encode the starting position and each move to the right as $\color{red}1$ while a move to the left is $\color{blue}0$. (This leads to the familiar binary representation of the Calkin-Wilf sequence.)

Now, if we move to the right, we move from $\frac ab$ to $\frac{a+b}b=\frac ab+1$. If we make $n$ consecutive steps to the right, we move from $\frac ab$ to $\frac ab+\color{red}n$, i.e. we effectively add $n$. If we move to the left, we move from $\frac ab$ to $\frac a{a+b}$, which is the same as $\frac1{1+\frac ba}$. $n$ steps to the left means moving from $\frac ab$ to $\frac1{\color{blue}n+\frac ba}$.

Now, hopefully this already rings a bell: this will lead to continued fractions! Let's take as an example $\frac 37$ which, as a continued fraction, looks like so: $$ 0 + \frac1{2+\frac13} = [0;2,3] $$ We can view this representation, reading it backwards, as a means to navigate the tree from the top. To reach $3$, you need three $\color{red}1$s. (The first one is for the starting point $\frac11$, the other two are to go from there to $\frac11+\color{red}2$.) To go from $3$ to $\frac1{\color{blue}2+\frac13}$, you need two $\color{blue}0$s. At that point, you're already done; the last zero means you don't need to take any more "$\color{red}1$ turns".

Here's another example. $\frac{19}{11}$ is $$ 1 + \frac1{1+\frac1{2+\frac1{1+\frac12}}} = [1;1,2,1,2] $$ Reading $[1;1,2,1,2]$ backwards translates to two $\color{red}1$s ($\frac{\color{red}2}1$), one $\color{blue}0$ ($\frac1{\color{blue}1+\frac12}=\frac23$), two $\color{red}1$s ($\frac23 + \color{red}2=\frac83$), one $\color{blue}0$ ($\frac1{\color{blue}1+\frac38}=\frac8{11}$), and finally one $\color{red}1$ ($\frac8{11}+\color{red}1=\frac{19}{11}$).

So, to reach any rational number, compute its continued fraction and read it backwards which'll give you a way to navigate the Calkin-Wilf tree and find the number, thereby re-creating the number, step by step, from the continued fraction. This also proves that every positive rational number actually occurs in the tree.

There's one small catch which is that you obviously must start with $\color{red}1$s and end with $\color{red}1$s (possibly, as in the first example, with zero $\color{red}1$s). Which means the continued fraction needs to consists of an odd number of pieces. This is not a problem, but rather a good thing. There are exactly two continued fraction representations for each rational number, and exactly one of them is the one we need. (For example, $\frac38$ can be written as $[0;2,1,2]$, which won't work, but also as $[0;2,1,1,1]$, which is what we need.) This proves uniqueness in the Calkin-Wilf tree.

Answer 2

I know this is old thread but I can't help to mention that it may not need to be this complicated. For any positive rational number $\frac{m}{n}$ in its simplest form, if $m>n$ we know it is a right-side child node and the parent should be $\frac{m-n}{n}$; otherwise it is a left-side child node and the parent is $\frac{m}{n-m}$. The path from $\frac{m}{n}$ to the root 1 is thus unique and can be found easily by repeatedly applying this strategy. This is exactly the algorithm to find $\gcd(m,n)$ by Euclidean Division, and since $m$ and $n$ are coprime, it is guaranteed to end up with the root (ie, $m=n=1$).

Answer 3

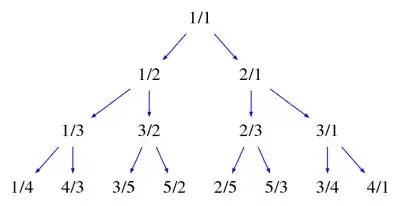
Definition: The Calkin-Wilf tree is an infinite binary tree in which each vertex is associated with a positive rational number expressed as an irreducible fraction $a\over b$; in particular, the number $1 \over 1$ is associated with the root vertex. Each vertex $a \over b$ has a left child whose value is $a \over a+b$ and a right child whose value is $a+b \over b$.

Observation 1: Each vertex has a left child whose value is less than 1, since $a<a+b$. Similarly, each vertex has a child on the right whose value is greater than 1.

Observation 2: The sum of the numerator and denominator of the first child is $2a+b$, while that of the second child is $a+2b$; in both cases the sum is greater than that of the parent $a+b$. It follows that by going down the tree, a strictly increasing sequence of sums is always obtained. On the contrary, going up the tree always results in a strictly decreasing sequence of sums.

I propose the following proofs.

Every rational number appears at least once

The parent of any rational number can be determined after expressing the number as an irreducible fraction $p \over q$, i.e. such that the greatest common divisor of $p$ and $q$ is 1. If ${p \over q}<1$, the parent of $p \over q$ is $p \over {q-p}$; if ${p \over q}>1$, the parent of $p \over q$ is ${p-q} \over q$. Therefore, the parent is a fraction whose sum of numerator and denominator is either $p$ or $q$, and in both cases it is less than $p+q$, which is the sum corresponding to the child fraction $p \over q$. It follows that a repeated reduction of this type must sooner or later reach the irreducible fraction with minimum sum, that is, the number $1 \over 1$. This is an informal proof that every rational number appears at least once as the vertex of the tree.

More simply: Among the fractions that do not appear in the tree, let $p \over q$ be the fraction with minimal sum $p+q$. If ${p \over q}=1$ then it appears at root, contradiction. If ${p \over q}>1$ then $p-q \over q$ does not appear, otherwise its right children would be $p \over q$. If ${p \over q}<1$ then $p \over {q-p}$ does not appear, otherwise its left children would be $p \over q$. In both cases there is a fraction not appearing whose sum ($p$ or $q$) is less than the minimal, which is a contradiction.

Any rational number can appear at most once

Furthermore, the parent formula provides for each step a unique sum value which is lower than the previous one, therefore, given any rational number, the sequence of sums to go up from the associated vertex to the root is unique and strictly decreasing (as already observed above). Assume there are two distinct vertices with the same rational number. Due to the structure of tree graphs, going up the tree from each one would sooner or later arrive at the same vertex. Since the sequence of sums is strictly decreasing, the number of steps taken to reach this vertex from each of the two starting vertices must be the same, otherwise we would have two distinct sum values for this vertex. In other words, the two sequences of sums, as well as being equal, are also synchronized. It follows that the two children of the common vertex (which correspond to the previous step of the sequences) have the same sum value, which is in contradiction with the definition of the tree. The conclusion is that no two vertices with the same rational number can exist, that is, a certain rational number can appear at most once in the tree.

More simply: In the first place $1 \over 1$ cannot appear more than once, because any vertex $1 \over 1$ below $1 \over 1$ at root would have the same sum, but any path down is a strictly increasing sequence of sums. Among the fractions that appear at least twice in the tree, let $p \over q$ be the fraction with minimal sum $p+q$. If ${p \over q}>1$ then the parent $p-q \over q$, which has sum $p$ less than $p+q$, appears at least twice, contradicting the minimality of the sum. Similarly if ${p \over q}<1$.

Overall, therefore, each rational number appears exactly once in the tree in the form of an irreducible fraction.