I would like to resolve this exercise: Let $W$ be a Brownian motion with $T_1=1 \text{ year}$ and $T_2=2 \text{ years}$.
I want to compute the probability that $W_{T_1}$ be positive and $W_{T_2}$ negative.
What I did:
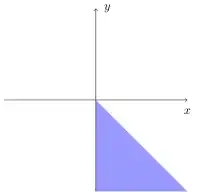
$X=W_{T_1}$ and $ Y=W_{T_2}-W_{T_1} $ independent $\sim$ Gaussian So our probability is: $$P(X>0,X+Y<0)=\int_0^{+\infty} \int_{-\infty}^{-x} \frac{1}{2 \pi} e^{- \frac{1}{2} (x^2+y^2)} \, dx \, dy $$
But I don't know how to continue.
Thanks for your help
Hint. Observe that if you set $$ f(x)=\int_{-\infty}^{-x} e^{- \frac{1}{2}y^{2}} dy\quad \text{then} \quad f'(x)=- e^{- \frac{1}{2}x^{2}} $$ and the initial integral takes the form $$ \begin{align} \int_{0}^{+\infty} \int_{-\infty}^{-x} \frac{1}{2 \pi} e^{- \frac{1}{2}(x^{2}+y^{2})} dx dy&=-\frac{1}{2 \pi}\int_{0}^{+\infty}f'(x)\cdot f(x)\:dx\\\\ &=-\frac{1}{4 \pi}\left[f^2(x)\right]_{0}^{+\infty}\\\\ &=\frac{f^2(0)}{4\pi} \qquad \left(\lim_{x\to+\infty}f(x)=0\right). \end{align} $$ One has $$ f(0):=\int_{-\infty}^0 e^{- \frac{1}{2}y^{2}} dy=\int_0^{\infty} e^{- \frac{1}{2}y^{2}} dy=\sqrt{\frac\pi2} $$ where we have used the standard gaussian integral result.
Then
$$ \int_{0}^{+\infty} \int_{-\infty}^{-x} \frac{1}{2 \pi} e^{- \frac{1}{2}(x^{2}+y^{2})} dx dy=\frac18. $$
The distribution of $(X,Y)$ is rotationally invariant, so the chance that it lies in the region $\{(x,y): x>0, x+y<0\}$ (shaded area below) is $1/8$.
