The equation for creating a quaternion from an axis-angle representation is $$x'= x \sin\left(\frac \theta 2\right)$$ $$y' = y \sin\left(\frac \theta 2\right)$$ $$z' = z \sin\left(\frac \theta 2\right)$$ $$w' = \cos\left(\frac \theta 2\right)$$ But why $\frac \theta 2$? Why not just $\theta$?
Asked
Active
Viewed 2,072 times
7
-
2Intuitively, because the quaternion representation of rotation works by conjugation, $qvq^$ where there are two $q^$ -- so there are two $q$s in the formula. If you had $\theta$ instead of $\theta/2$, an attempt to rotate by $180^\circ$ would produce $q=-1$, which commutes with $v$ and cancels out with its counterpart. – hmakholm left over Monica Feb 02 '16 at 11:01
-
Also relevant. – hmakholm left over Monica Feb 02 '16 at 11:02
1 Answers
7
Hint:
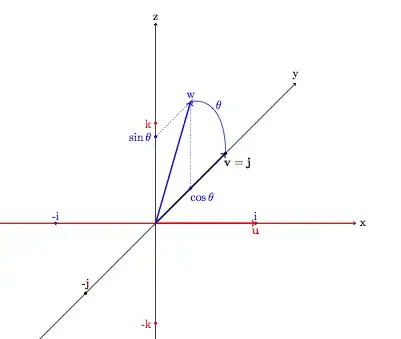
Consider the unitary quaternion $$ u=\cos \theta + \bf{i}\sin \theta $$ and the pure imaginary quaternion ${\bf j}$. Then the product: $ u{\bf j}u^* $ (where $u^*=\cos \theta - {\bf i}\sin \theta$ is the conjugate of $u$) is: $$ (\cos \theta + {\bf i}\sin \theta){\bf j}(\cos \theta - {\bf i}\sin \theta)= (\cos \theta + {\bf i}\sin \theta)({\bf j}\cos \theta + {\bf k}\sin \theta)= $$ $$ =(\cos^2 \theta -\sin^2 \theta){\bf j}+2{\bf k}\cos \theta \sin \theta = {\bf j}\cos 2 \theta+{\bf k} \sin 2 \theta $$ that is the vector ${\bf j}$ rotated by an angle $2 \theta$ around the ${\bf i}$ axis.
Now, do the same for the other axis ${\bf j}$ and ${\bf k}$ and extend this result to any rotation around an axis ${\bf u}= u_1{\bf i}+u_2{\bf j}+u_3{\bf k}$.
Emilio Novati
- 62,675