The starting problem was to prove $$\sin 26^{\circ}\sin 58^{\circ}\sin 74^{\circ}\sin 82^{\circ}\sin 86^{\circ}\sin 88^{\circ} \sin 89^{\circ}>\frac{45\sqrt{2}}{64\pi}\\\cos 1^{\circ}\cos 2^{\circ}\cos 4^{\circ}\cos 8^{\circ}\cos 16^{\circ} \cos 32^{\circ}\cos 64^{\circ}>\frac{45\sqrt{2}}{64\pi}\\128\sin 1^{\circ}\cos 1^{\circ}\cos 2^{\circ}\cos 4^{\circ}\cos 8^{\circ}\cos 16^{\circ} \cos 32^{\circ}\cos 64^{\circ}>\frac{90\sqrt{2}}{\pi}\sin 1 \\\sin 128^\circ>\frac{90\sqrt{2}}{\pi}\sin\frac{\pi}{180}$$ Now if $\frac{\pi}{180}>\sin(\frac{\pi}{180})$ is true then the inequality is true but I'm not sure how to prove the inequality.
Asked
Active
Viewed 155 times
2
-
5Possible proofs depend on the allowed resurces. The inequality is intuitive with the unit circle definitions (https://en.wikipedia.org/wiki/Trigonometric_functions#Unit-circle_definitions) for the first quadrant, where you have $\mathrm{sin} < \mathrm{chord} < \mathrm{arc},$ where $\mathrm{arc}$ is you argument angle in radians. – gammatester Feb 01 '16 at 11:18
-
2Allowed resources are unit circle definition,right angled triangle definition,most of trigonometric identities.Pretty much anything precalculus without differentiation and series.The solution seems nice – kingW3 Feb 01 '16 at 11:38
2 Answers
6
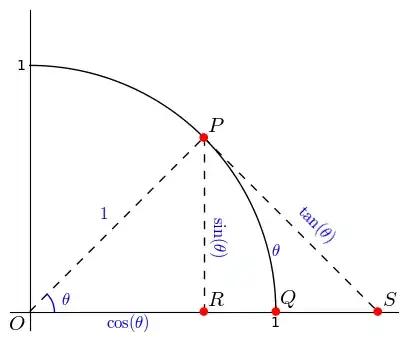
In the diagram below (borrowed from this answer), we have:
$\sin(\theta) < PQ$, because $PQ$ is the hypothenuse of the right triangle $PQR$,
$PQ < \theta$, because $PQ$ is the shortest distance from $P$ to $Q$,
and so $\sin(\theta) < PQ < \theta$.