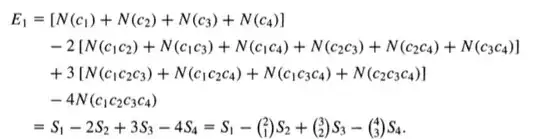1

I'm trying to understand where the combinations (the coeffecients of the $Si$'s) of this example come from.

enter image description here

From my understanding, the first example denotes the generalized inclusion exclusion using $3$ sets ($t=3$ denotes this) and $E_1$ is the number of sets such that exactly one of the three conditions $c_1,c_2,c_3$ are met. Similarly, $S_i$ denotes the number of elements such that $i$ conditions are met.

Here is another example for $t=4$.

enter image description here

vonbrand
  • 27,812
  • It appears to me that the author is just writing $n\choose{n-1}$ instead of $n$. It's not clear why the author wants to do that – maybe it becomes clear in some other part you haven't quoted – but it's clear that it's correct. – Gerry Myerson Jan 30 '16 at 09:32
  • 2
    This answer might be helpful: http://math.stackexchange.com/a/362516 – user84413 Jan 30 '16 at 19:05
  • @GerryMyerson: The author is correct, but could be more clear: notice that $\binom{n}{1}=\binom{n}{n-1}$ and the target is $E_1$, so the $\binom{n}{1}$ is for each $N(\dots)$ to find out who will need it to do IEP. – linear_combinatori_probabi Aug 31 '20 at 09:52

1 Answers1

4

The cleanest derivation I've seen is in Wilf's generatingfunctionology (third edition 2004, A. K. Peters).

Define objects having properties, a set is identified with a property (i.e., if $x \in A$, we say $x$ has property $A$). Call $N(\supseteq S)$ the number of objects having the properties in $S$ (and possibly others). It is easy to compute the values:

$\begin{align} N_r = \sum_{\lvert S \rvert = r} N(\supseteq S) \end{align}$

i.e., add up all the $N(\supseteq S)$ for $r$ properties.

Call $e_t$ the number of objects with exactly $t$ properties, typically we set up things so we are interested in $e_0$, number of objects without any properties.

We want to relate $N_r$ with the $e_t$. An object with exactly $t$ properties will be counted $\binom{t}{r}$ times when counting $N_r$, so:

$\begin{align} N_r = \sum_{t} \binom{t}{r} e_t \end{align}$

Define generating functions:

$\begin{align} N(z) &= \sum_r N_r z^r \\ E(z) &= \sum_t e_t z^t \end{align}$

From the above:

$\begin{align} N(z) &= \sum_{r} N_r z^r \\ &= \sum_r \sum_t \binom{t}{r} e_t z^t \\ &= \sum_t e_t \sum_r \binom{t}{r} z^t \\ &= \sum_t e_t (1 + z)^t \\ &= E(z + 1) \end{align}$

From here you get the magic formula:

$$E(z) = N(z - 1)$$

In particular, you have:

$\begin{align} e_0 &= E(0) \\ &= N(-1) \\ &= \sum_r (-1)^r N_r \\ e_t &= [z^t] E(z) \\ &= [z^t] N(z - 1) \\ &= \sum_r N_r [z^t] (z - 1)^r \\ &= \sum_r (-1)^{r - t} \binom{r}{t} N_r \end{align}$

Your binomial coefficients materialized.

The advantage is that it is often easy to work with $N(z)$ directly, and get $e_0$. The formula for $e_t$ is messy, but very easy to derive by this route on the fly if needed.

vonbrand
  • 27,812