1

I was trying to prove this inequality $\left|x\right| < \left|\tan(x)\right|$ in a neighborhood of $0$. I tried splitting into the four cases opening the modulus but still wasnt able to solve it. I dont know if it is possible using MVT or other calculus theorems. Sketching a graph I see it is true but how to prove it analitically?

Frentos
  • 3,041
Marteen
  • 11
  • 1

5 Answers5

4

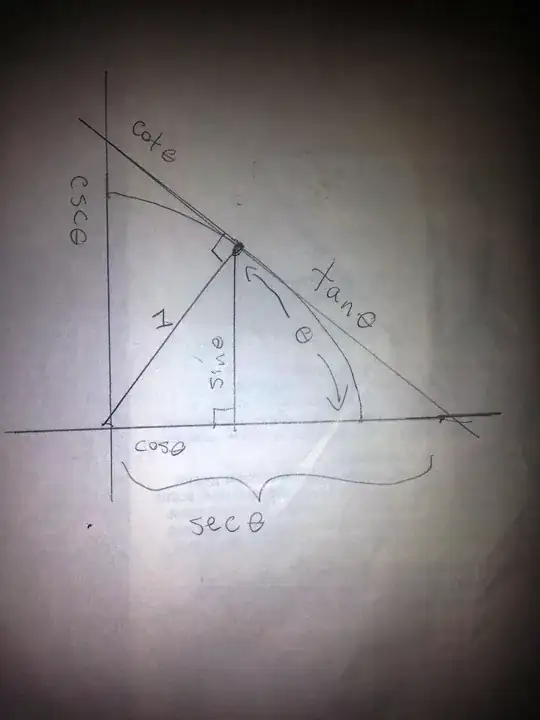
This isn't a formal proof, but its a nice geometrical relation that shows the identity holds.

Edit: I'd like to thank Yves Daoust for pointing a flaw in my reasoning.

The proper way to view this image as evidence that the identity holds is to compare areas. Thea area of a sector of the unit circle subtended by an angle $\theta$ is $\frac{1}{2}\theta$. The are the right triangle with side lengths $(1,\tan(\theta),\sec(\theta))$ is $\frac{1}{2} \tan(\theta)$. Visually it is clear that the area of the triangle exceeds the area of the sector, which suggests that $\tan(\theta)>\theta$.

enter image description here

Spencer
  • 12,271
  • I apologize for the sloppy image, I'll add a nicer one later when I have the tools available to make one at hand. – Spencer Jan 29 '16 at 08:08
  • Sorry but I don't see how this figure establishes a relation between $\theta$ and $\tan(\theta)$. –  Jan 29 '16 at 08:15
  • $\theta$ is the labeled arc length along the circle. Compare this length with the line segment which has a length equal to $\tan(\theta)$. I'll try to edit the image to make this more clear. – Spencer Jan 29 '16 at 08:16
  • How do you compare a curve and a straight line ? I can agree for the chord, but not for the arc. (Changing the figure won't help.) –  Jan 29 '16 at 08:17
  • @YvesDaoust, I think you edited your comment for clarification while I was typing my response; either that or I just missed your point on my first reading. I see what you're saying. I'm going to leave this up for now, but if I can't think of a way to convince you over the next couple of days I will delete the answer. – Spencer Jan 29 '16 at 08:32
  • @YvesDaoust, compare areas instead of arc lengths. The area of the sector subtended by the circle is $\theta/2$. The area of the triangle which has side lengths $(1,\tan(\theta),\sec(\theta))$ is $\tan(\theta)/2$. The area of the triangle is clearly larger than the area of the sector. – Spencer Jan 29 '16 at 08:37
  • I agree with that. I could'nt guess it from the figure. You can indeed make it more explicit. –  Jan 29 '16 at 08:43
  • @YvesDaoust, thank you for correcting me. – Spencer Jan 29 '16 at 08:47
  • 1
    +1 for the geometrical approach. FWIW here is a related proof of mine using lengths instead of areas. – dxiv Jan 29 '16 at 23:48
1

We start from

$$\frac1{x^2+1}<1$$ for $x\in\left(0,\dfrac\pi2\right)$, and integrate

$$\int_0^x\frac{dt}{t^2+1}=\arctan(x)<\int_0^xdt=x.$$

As the tangent is a strictly increasing function, we have both

$$\arctan(x)<x$$ and $$x<\tan(x).$$

1

Suppose $0<x<\pi/2$; by the mean value theorem, there exists $c\in(0,x)$ such that $$ \frac{\tan x}{x}=\frac{1}{\cos^2c} $$ so $$ \frac{x}{\tan x}=\cos^2c<1 $$ that yields $x<\tan x$.

The case $-\pi/2<x<0$ is now easy.

egreg
  • 238,574
0

$\tan x=\sin x/\cos x$ and so it's odd. Suppose you prove $x<\tan x$ for $0<x<a$; it follows than $|x|<|\tan x|$ for $-a<x<0$. We have $d(x-\tan x)/dx=-\tan^2 x<0$, so $x-\tan x< 0-\tan 0=0$ and $\tan x$ is $> x$ for small positive $x$.

ForgotALot
  • 3,931
0

Preliminary observation: The inequality you say is not strict for $x=0$. We shall therefore prove that it is strict for $x\in(-\varepsilon,0)\cup(0,\varepsilon)$.

Since both functions are odd, you just need to consider the case $x>0$.

$$\lim_{x\to 0}\frac{\tan x-x}{x^3}\stackrel{\text{l'H}\hat{\text{o}}\text{pital}}=\lim_{x\to 0}\frac{1+\tan^2x-1}{3x^2}=\lim_{x\to 0}\frac13\left(\frac{\tan x}{x}\right)^2=\frac13$$

This implies that, for sufficiently small $\varepsilon>0$ and for every $x\in(0,\varepsilon)$, it holds $$\frac{\tan x-x}{x^3}>\frac16$$

Hence, for $x\in (0,\varepsilon)$, it holds $$\tan x>x+\frac{x^3}{6}>x$$.