13

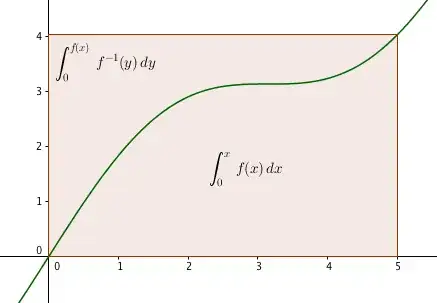
Suppose that the function $f:[0,\infty)\rightarrow\mathbb{R}$ is continuous and strictly increasing and that $f:(0,\infty)\rightarrow\mathbb{R}$ is differentiable. Moreover, assume $f(0)=0$. Consider the formula $$\int_{0}^{x}f+\int_{0}^{f(x)}f^{-1}=xf(x)\qquad\text{for all $x\geq0$}$$ Prove this formula.

Attempt: Consider that $g(x)=\int_{0}^{x}f+\int_{0}^{f(x)}f^{-1}-xf(x)$ which is continuous on $\mathbb{R}$. Then differentiate $g(x)$, we have $g'(x)=f(x)+xf'(x)-f(x)-xf'(x)=0$. Thus for all $x$, $$g(x)-g(0)=0\Longrightarrow\int_{0}^{x}f+\int_{0}^{f(x)}f^{-1}-xf(x)=0$$

I am not sure my the equality valid not or not. If not, can someone give me a suggestion to modify the proof. Thanks.

Simple
  • 3,593
  • 1
    looks good to me – David Kleiman Jan 29 '16 at 02:53
  • 1
    Your proof looks good, although you may want to replace "$g$ is continuous" by "$g$ is continuous on $[0,\infty)$ and differentiable on $(0,\infty)$," since then you do differentiate it. Also, you basically prove that $g$ is constant on $(0,\infty)$, so to say that it's constant and equal to $g(0)$, then you have to invoke its continuity at $0$. – Clement C. Jan 29 '16 at 02:53

2 Answers2

5

I think your proof is fine. Here is an alternative.

If you are willing to interpret an integral as area, then look at the plot of $y=f(x)$. It is anchored at $(0,0)$, and increasing. $xf(x)$ is the area of a rectangle with lower left corner at $(0,0)$.

The two integrals are the area under the curve, and the area to the left of that curve (integrating with respect to $y$).

enter image description here

(OK, the picture abuses "$x$" in the lower integral. Maybe the indexing variable should be "$t$" or something other than "$x$".)

2'5 9'2
  • 54,717
2

By the transformation $u=f^{-1}(y)$, \begin{align*} \int_0^{f(x)} f^{-1}(y) dy &= \int_0^x uf'(u) du\\ &=uf(u)|_0^{x} - \int_0^xf(u) du \end{align*} $$$$ Generally, in Riemann-Stiltjes integral sense without the differentiability assumption, \begin{align*} \int_0^x f(u)\,du + \int_0^x u\, df(u) = xf(x), \end{align*} by noting that \begin{align*} \sum_{i=1}^nf(x_{i-1})(x_i-x_{i-1}) + \sum_{i=1}^n x_i [f(x_i)-f(x_{i-1})] &= \sum_{i=1}^n\big[x_if(x_i) - x_{i-1}f(x_{i-1})\big]\\ &= xf(x), \end{align*} where $0=x_0 < x_1 < \cdots < x_n = x$ is a partition of the interval $[0,\, x]$.

The conclusion now follows immediately.

Gordon
  • 4,461