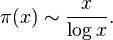3

Given some arbitrarily large $a$, what is the probability that this number is a prime number?

My attempt involves seeing that for $a$ to be prime, then it must not have a factor $N$ in the following range:

$$2\le N\le\sqrt{a}$$

Which helps make the problem somewhat easier.

Then, I noted all the possible prime numbers in the range for needed factors.

I will call them $p_1,p_2,p_3,\dots p_i$.

I think, if I am correct, that the probability that $a$ will be prime is as follows:

$$P_a=\frac1{\Pi_{v=1}^ip_v}$$

Of course, this requires knowledge on all of the primes in the given range, which I want to avoid.

So my questions are, is my probability correct? And is there another formula that finds the probability of a number $a$ being prime without the need of anything other than the given number $a$?

Note that the probability of a number being prime is not the same as the question whether or not a number is prime.

Ok, according to the comments, I should probably clarify things. If this helps, I wish to find the probability that a given number is prime, and I want to find the individual probability of each natural number in terms of itself.

That is, the probability $P_a$ that $a$ will be prime is given as:

$$P_a=f(a)$$

Where we apply some operation to find the probability that $a$ is prime.

To clarify what I mean by probability of a number being prime, I mean that given a number prime, how probable is it to be prime? (sorry for confusions).

For example, can we agree that $10$ is more likely to be prime than $100$? It is apparent that numbers that are smaller are more often prime numbers than large numbers.

So, it might be interesting to notice that:

$$P_{10}>P_{100}>P_{100+n}$$

Still confused? Or perhaps this question is just unanswerable.

So I ask a second question, one that may be more clear.

In a given range, $a\le N\le b$, how many prime numbers $N$ are expected to exist in that range? I think that this second question is clearer, but if it still raises concerns, do inform me.

Simply Beautiful Art
  • 74,685
  • 4
    What probability distribution are you using on the positive integers? – Chappers Jan 28 '16 at 00:40
  • @Chappers I don't really know what that means, so I probably can't answer your question. Could you try to explain? – Simply Beautiful Art Jan 28 '16 at 00:41
  • 2
    In order to discuss probability, you must have a probability distribution. For example, what is the probability of picking a $7$? –  Jan 28 '16 at 00:45
  • @ElliotG Roughly though. I am of course aware of the prime counting function, but I also note that to say that it is roughly $\ln(n)$ doesn't work for large $n$. Also, that is interesting. You gave me a range in which an approxiamate amount of numbers will be prime. – Simply Beautiful Art Jan 28 '16 at 00:45
  • To clarify, I believe I am asking for univariant distribution. – Simply Beautiful Art Jan 28 '16 at 00:47
  • 2
    There are infinitely many natural numbers, which means that you can't just assign each one the same positive probability of being chosen. So you have to specify the probability with which each one may be picked. An obvious one is to give $n$ a chance proportional to $n^{-s}$ for some $s>1$, which will obviously take you to the Riemann zeta-function. – Chappers Jan 28 '16 at 00:48
  • But, for example, if you put all natural numbers in a bag, what is the probability for select 1? Whitout a probability distribution, the ask doesn´t have sense. – sinbadh Jan 28 '16 at 00:49
  • Um, does it help to say I want to know the probability of the number I pick from the bag being prime in terms of the number I chose? I want a formula that finds the probability a given number is prime, which obviously decreases rapidly as we choose larger numbers? – Simply Beautiful Art Jan 28 '16 at 00:51
  • @ElliotG: There are roughly $n/\ln n$ primes less than $n$, not roughly $\ln n$. – Eric Wofsey Jan 28 '16 at 00:51
  • 4
    It's not clear to me what is meant by "the probability that a given number is prime". A given number is either prime or not. I suggest you give some thought to what you really want to know. For example, a sensible question (perhaps not the question you want) would be: "a number is chosen uniformly and at random from all $n$-digit numbers: what, in terms of $n$, is the probability that it is prime?" – David Jan 28 '16 at 00:53
  • 1
    I think a better word than "probability" is "density." I think this article gives you a good description of what you're looking for https://en.m.wikipedia.org/wiki/Prime_number_theorem – Paul Jan 28 '16 at 01:08
  • Hmm, I'm reading about the Prime Number Theorem. I might close this question if I find an answer satisfying enough to me. – Simply Beautiful Art Jan 28 '16 at 01:08
  • @Paul Nice timing. XD – Simply Beautiful Art Jan 28 '16 at 01:08
  • 2
    Are people misunderstanding this on purpose? It seems like a simple enough question. – user41728 Jan 28 '16 at 01:09
  • 2
    @user41728: No. The problem is that the question would not even arise if the asker had understood probability properly. That is what all the commenters are trying to get at. To give an analogy, it is ill-defined to ask "What is the probability that a random integer is more than $100$?". The answer is "What is random???". – user21820 Jan 30 '16 at 03:44
  • See also: Percentage of primes among the natural numbers – Martin Sleziak Dec 07 '22 at 14:22

3 Answers3

8

The proportion of the first $N$ positive integers which are prime goes to $0$ as $N \to \infty$. This is because the proportion of the first $N$ positive integers which are not divisible by the first $k$ primes $p_1, p_2, \dots p_k$ is, as $N$ gets large,

$$\prod_{i=1}^k \left( 1 - \frac{1}{p_i} \right)$$

and this product goes to $0$ as $k \to \infty$. This is a nice exercise.

So in some sense the probability is $0$ (more precisely, the natural density; this shares some but not all of the features of a probability measure).

But in a more useful sense, according to the prime number theorem, the probability that a positive integer about as large as $N$ is prime is about $\frac{1}{\ln N}$.

Qiaochu Yuan
  • 419,620
  • My understanding is that the prime number theorem only says that the number of primes $\leq N$ is around $\frac{N}{\log N}$. However, these primes are (obviously) not distributed uniformly in ${1,2, ... , N}$. There's proportionally more primes near small values of $n$, than near $N$, when $N$ is large. Thus $\frac{1}{\log N}$ would be an overestimate for the "probability that a positive integer about as large as $N$ is prime". – MathematicsStudent1122 Oct 02 '19 at 04:27
  • That's a good guess, but it actually turns out to be more accurate than that argument suggests: https://en.wikipedia.org/wiki/Prime_number_theorem#Prime-counting_function_in_terms_of_the_logarithmic_integral – Qiaochu Yuan Oct 02 '19 at 06:33
2

Since $\pi(x) \sim \frac{x}{\log(x)}$, we can approximate the probability some $n$ is prime by computing the limit $$\lim_{x \to 0} \frac{\frac{n+x}{\log(n+x)} - \frac{n-x}{\log(n-x)}}{2x}.$$ Applying L'Hôpital's rule, we obtain $\frac{\log(n) - 1}{\log(n)^2}$.

Archsys
  • 21
  • isn't it should be something like (log(abs(n))−1)/(log(abs(n))^2) because prime number sequence is symmetric around 0 ? – zb' Jan 25 '21 at 05:44
1

See the Prime Number Theorem:

Prime number theorem

Daniel R. Collins
  • 8,380
  • This only gives the probability that some number in the range up to $x$ is prime. Calculating the probability for $x$ itself is a little more involved is it not? – it's a hire car baby Oct 10 '18 at 07:25