2

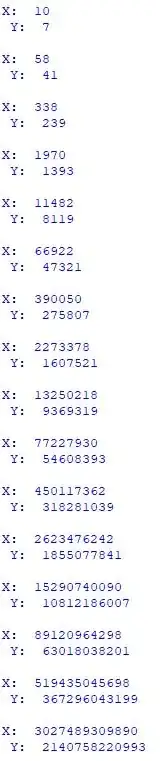
I'd love your help with finding all the integer solutions to the following equation:

$x^2 - 2y^2 =2 $. I want to use Pell's theorem so I changed the equation to $-\frac{1}{2}x^2+ y^2 =-1$, Can I use Pell's Theorem now? I got a private solution for $-\frac{1}{2}x^2+ y^2 =1$ $y=3, x=4$, so form Pell I get that $\alpha= (4+3\sqrt{2})^n$ for every integer $n$, and a private solution for $-\frac{1}{2}x^2+ y^2 =-1$ is $y=1, x=2$, so the total solution is $\alpha= (1+\sqrt{2}) \cdot (+/- (4+3\sqrt{2})^n)$. Are all these steps correct? and if not- how should I solve this one?

Thank you!

Jozef
  • 7,100

4 Answers4

9

The standard way is to find one solution to $x^2-2y^2=2$, e.g., $x=2$, $y=1$, and find the fundamental solution to $x^2-2y^2=1$, which is $x=3$, $y=2$, and then go $(2+\sqrt2)(3+2\sqrt2)^n$, etc., etc.

Gerry Myerson
  • 179,216
  • Thank you. what would the answer would be if the original equation was $x^2-2y^2=-2$ should I do the same and find fundamental for $x^2-2y^2=-1$ which is $(1+\sqrt{2})(3+2 \sqrt{2})^n$ and multiply it with a praticular solution for $x^2-2y^2=-2$? – Jozef Jun 24 '12 at 08:09
  • That would also give you solutions for $x^2-2y^2=2$. To solve $x^2-2y^2=-2$, you need a particular solution of $x^2-2y^2=-2$ with a solution of $x^2-2y^2=1$, or a particular solution of $x^2-2y^2=2$ with a solution of $x^2-2y^2=-1$. Think about how these solutions work, about the norms you get! – Gerry Myerson Jun 24 '12 at 09:18
1

Pell's Theorem is only valid for integer coefficients - so no.

Nathaniel Bubis
  • 33,018
0

Let's say $\alpha_n$ and $\beta_n$ the $n$-solution of the equation $x^2 - 2y^2 = 2$. We have: $$\left\{\begin{matrix} \alpha_0 = 2 \\\beta_0 = 1 \end{matrix}\right. \land \left\{\begin{matrix} \alpha_1 = 10 \\\beta_1 = 7 \end{matrix}\right. \land \left\{\begin{matrix} \alpha_2 = 58 \\\beta_2 = 41 \end{matrix}\right.$$

From here, you can deduce the recoursive relation: $$\left\{\begin{matrix} \alpha_{n} = 3\alpha_{n-1}+4\beta_{n-1} \\\beta_{n} = 2\alpha_{n-1}+3\beta_{n-1} \end{matrix}\right.$$

This is the list of the values of $\alpha_n$ and $\beta_n$:

enter image description here

Matteo
  • 6,581
0

Another way is to note that $x$ has to be even. Hence if $x=2x_1$, we get that $$2x_1^2-y^2 = 1 \implies y^2 - 2x_1^2 = -1 \implies \left(y + \sqrt2 x_1\right)\left(y - \sqrt2 x_1\right) = -1$$ Now clearly, one solution is $(x_1,y) = (1,1)$. Raise both sides to any odd power, i.e., $$\left(y + \sqrt2 x_1\right)^{2n-1}\left(y - \sqrt2 x_1\right)^{2n-1} = (-1)^{2n-1} = -1$$ and note that $$\left(y + \sqrt2 x_1\right)^{2n-1} = Y_n(y,x_1) + \sqrt2 X_n(y,x_1)$$ $$\left(y - \sqrt2 x_1\right)^{2n-1} = Y_n(y,x_1) - \sqrt2 X_n(y,x_1)$$ which in turn gives us infinite other solutions since $$Y_n^2 -2 X_n^2 = -1$$