Limit $\lim_{x \to 1} \frac{\log{x}}{x-1}$ without L'Hôpital

Question

I was wondering if it's possible to identify this limit without using L'Hôpital's Rule: $$\lim_{x \to 1} \frac{\log{x}}{x-1}$$

Note that $\log 1 = 0$, so you are evaluating $\log'$ at $x=1$. — copper.hat, Jan 22 '16 at 17:18
Since this is precisely the limit of the difference quotient that defines the derivative of $\log x$ at $x=1$, it might motivate your Readers a little to know why you want to avoid l'Hôpital in this situation. — hardmath, Jan 22 '16 at 17:19

score 9 · Accepted Answer · edited Apr 13 '17 at 12:20

9

In THIS ANSWER and THIS ONE I showed, without the use of calculus, that the logarithm function satisfies the inequalities

$$\frac{x-1}{x}\le \log(x)\le x-1$$

Therefore, we can write for $x>1$

$$\frac1x \le \frac{\log(x)}{x-1}\le 1$$

and for $x<1$

$$1 \le \frac{\log(x)}{x-1}\le \frac1x$$

whereupon applying the squeeze theorem yields the result $1$.

edited Apr 13 '17 at 12:20

Community

1

answered Jan 22 '16 at 18:03

Mark Viola

179,405

1

An elegant one! – Laurent Duval Jan 22 '16 at 18:06
@LaurentDuval Laurent. Thank you! Much appreciated. - Mark – Mark Viola Jan 22 '16 at 19:35

score 5 · Answer 2 · answered Jan 22 '16 at 17:30

To elaborate on copper.hat's comment, it does not require L'Hopital's rule to recognize that

$$\lim_{x\to1}{\log x\over x-1}=\lim_{x\to1}{\log x-\log1\over x-1}=f'(1)\quad\text{where }f(x)=\log x$$

This is simply the definition of the derivative. If you also know that $f'(x)=1/x$, then you get

$$\lim_{x\to1}{\log x\over x-1}=1$$

It might be noted that L'Hopital's rule is often invoked for problems like this, but its invocation is purely a matter of convenience.

score 3 · Answer 3 · answered Jan 22 '16 at 17:19

Rewrite this using $t = h-1$ as $$\lim_{t\to 0} \frac{\log(1+t) - 0}{t}.$$

Now try to recognize this as the derivative of a function you know.

The point of this exercise is almost certainly to recognize that this is the definition of the derivative.

score 3 · Answer 4 · edited Jan 22 '16 at 17:27

3

It's simple:

$$\lim_{x \to 1} \frac{\log{x}}{x-1}$$ $$=\lim_{(x-1) \to 0} \frac{\log{[1+(x-1)]}}{(x-1)}$$ $$=\lim_{u \to 0} \frac{\log{(1+u)}}{u}$$ $$= \log'(0)$$ $$=1$$

The last step comes from this link.

edited Jan 22 '16 at 17:27

Nizar

2,782

answered Jan 22 '16 at 17:20

SchrodingersCat

24,472

1

why is the last step obvious -- you have a 0/0 form? – gt6989b Jan 22 '16 at 17:22
1

This is the derivative of $u\mapsto \ln(1+u)$ at $0$. I.e., $\frac{1}{1+0}=1$. – Clement C. Jan 22 '16 at 17:23
@gt6989b It's a common limit used often. – SchrodingersCat Jan 22 '16 at 17:23
4

Think you mean $\log^{'} 1$ – πr8 Jan 22 '16 at 17:28
2

It's curious that you posted an answer and voted to close the post. ;-)) – Mark Viola Jan 22 '16 at 19:40

score 2 · Answer 5 · answered Jan 22 '16 at 17:21

2

If you're looking to avoid relying on knowing derivatives already, you can write $\frac{\log x}{x-1}=\frac{\int_1^x\frac{dt}{t}}{x-1}$, showing it to be the mean value of $\frac{1}{t}$ for $t\in[1,x]$. Take $x\to1$ to show that the limit is equal to $1$.

answered Jan 22 '16 at 17:21

πr8

10,800

Well, the use of integrals kind of embeds derivatives through the FTC, does it not? ;-) - Mark – Mark Viola Jan 22 '16 at 19:37

score 1 · Answer 6 · answered Jan 22 '16 at 17:19

1

Hint

Decompose the logarithm into Taylor series around $1$.

answered Jan 22 '16 at 17:19

gt6989b

54,422

3

Umm, this avoids l'Hôpital (one derivative) by taking derivatives of all orders? – hardmath Jan 22 '16 at 17:20
@hardmath you only need up to the quadratic term. The OP was not interested in minimizing the number of derivatives, just in avoiding to use L'Hospital's rule... – gt6989b Jan 22 '16 at 17:21
1

I will let the OP speak for what they wanted to avoid, but to me (see my Comment) it appears the request was to avoid taking any derivatives. So when a number of answers are proposed to use the Taylor series instead, I'm not sure it is in the spirit of the Question. – hardmath Jan 22 '16 at 17:24

score 1 · Answer 7 · answered Jan 22 '16 at 17:20

1

$$\lim_{x \to 1} \frac{\log{x}}{x-1}\quad\iff\quad\lim_{x\to 0}\frac{\log(x+1)}{x}$$

Using Taylor expansion we get

$$\lim_{x\to 0}\frac{x-x^2/2+O(x^3)}{x}=\lim_{x\to 0}(1-x/2+O(x^2))=1$$

answered Jan 22 '16 at 17:20

Kamil Jarosz

4,984

BTW, you don't need the quadratic term, only $x+o(x)$. – Clement C. Jan 22 '16 at 17:24
3

This is l'Hospital's rule, just thinly wrapped as Taylor expansion. – Snow Jan 22 '16 at 17:27

Shaswata · Answer 8 · 2016-01-22T17:59:19.767

1

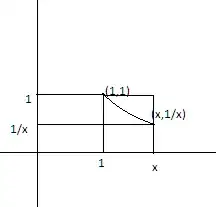
From the above image it is easy to observe that, $$\frac{x-1}{x}<\int^{x}_{1}t dt<x-1$$

Since Area of smaller rectangle< Area under curve< Area of larger rectangle,

$$\rightarrow \frac{1}{x}<\frac{log(x)}{x-1}<1$$

$lim_{x \rightarrow 1} \frac{1}{x}=1$

Hence by Sandwich Theorem $lim_{x \rightarrow 1} \frac{log(x)}{x-1}=1$

edited Jan 22 '16 at 17:59

answered Jan 22 '16 at 17:53

Shaswata

5,068

Those inequalities for the logarithm can be established without the use of calculus. ;-) - Mark – Mark Viola Jan 22 '16 at 19:38

Limit $\lim_{x \to 1} \frac{\log{x}}{x-1}$ without L'Hôpital

8 Answers8