Which of the numbers $300!$ and $100^{300}$ is greater

Question

Determine which of the two numbers $300!$ and $100^{300}$ is greater.

My attempt:Since numbers starting from $100$ to $300$ are all greater than $100$. But am not able to justify for numbers between $1$ to $100$

Answer 1

Take the logarithm of each side, base $100$. Since the $\log$ function is monotonically increasing, this preserves the ordering. $\log_{100}(100^{300})$ is clearly $300$. Meanwhile,

$$\log_{100}300! = \log_{100}1 + \log_{100}2 + \dotsb + \log_{100}300 = \sum_{n=1}^{300} \log_{100}n .$$

We can try using integrals to approximate this series. Since, again, $\log$ is monotonically increasing, we have:

$$\sum_{n=1}^{300} \log_{100}n \geq \int_{1}^{300} \log_{100}x\, dx = \dfrac{1}{\ln 100} \int_{1}^{300} \ln x\, dx = \dfrac{1}{\ln 100} \left[x \ln x - x \right]^{300}_1 = \dfrac{300\ln 300 - 299}{\ln 100} = 306.64... > 300.$$

This implies that $300! \geq 100^{300}.$

Answer 2

$\displaystyle e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+\frac{x^{n+1}}{(n+1)!}+\cdots $

$$e^x>\frac{x^n}{n!}$$ for $x=n$

$$n!>\bigg(\frac{n}{e}\bigg)^n>\bigg(\frac{n}{3}\bigg)^n$$

for $n=300.$ we have $\color{red}{300!>(100)^{300}}$

Answer 3

$n! > (n/e)^n$ so $300! >(300/e)^{300} > 100^{300} $ since $e < 3$.

To show $n! > (n/e)^n$, it is true for $n=1, 2$, and $3$.

If it is true for $n$ and false for $n+1$, then $n! > (n/e)^n$ and $(n+1)! \le ((n+1)/e)^{n+1}$ so, dividing, $n+1 < \frac{((n+1)/e)^{n+1}}{(n/e)^n} = \frac{(n+1)^{n+1}}{en^n} $ or $e < (1+1/n)^n $ which is false.

Note that this proof can be easily modified to use $e > (1+1/n)^n $ to show that $n! > (n/e)^n$ implies that $(n+1)! > ((n+1)/e)^{n+1}$.

Answer 4

The easiest way is to collect values in some optimal way.

$$\frac{300!}{100^{300}}=\prod\limits_{k=1}^{300}\frac{k}{100}$$

Let us reduce this by noticing that we can replace $300\cdot 299 \cdot 298 \cdot ... \cdot 292 \cdot 291$ with $290^{10}$ and similarly in each section of 10 by 10 the same switch getting

$$\frac{300!}{100^{300}}=\prod\limits_{k=1}^{300}\frac{k}{100}>\frac{10!}{10^{10}}\prod\limits_{k=1}^{29}\frac{(10k)^{10}}{100^{10}}$$

We can continue simplification:

$$\frac{300!}{100^{300}}>\frac{10!}{10^{10}}\prod\limits_{k=1}^{29}\frac{10^{10}k^{10}}{10^{20}}=\frac{10!}{10^{10}}\prod\limits_{k=1}^{29}\frac{k^{10}}{10^{10}}=\frac{10!(29!)^{10}}{10^{300}}$$

Since we expect a big difference we will ignore $10!$ and continue

$$\frac{10!(29!)^{10}}{10^{300}}>\frac{(29!)^{10}}{10^{300}}$$

We want to prove that $\frac{(29!)^{10}}{10^{300}}> 1$ which means in essence that we expect $$\frac{29!}{10^{30}}>1$$

We can further continue by replacing $29!$ with $(28!!)^2$ of course knowing $29! > (28!!)^2$

$$\frac{29!}{10^{30}}>\frac{(28!!)^2}{10^{30}}$$

This can be reduced to

$$\frac{28!!}{10^{15}}=\frac{2^{14}14!}{10^{15}}$$

Now we just make a series of substitution. Knowing $2^{10}=1024>1000$ we have

$$\frac{2^{14}14!}{10^{15}}>\frac{2^{4}14!}{10^{12}}$$

Well now we have to resort to prime factorization but this is simple since we have it all

$$\frac{2^{4}\cdot 14\cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5^{12}2^{24}}$$

It all comes to

$$\frac{2^3\cdot 3^5\cdot 7^2\cdot 11\cdot 13}{5^{10}}$$

We can keep on replacing carefully $11$ with $10$ and $13$ with $12$

$$\frac{2^3\cdot 3^5\cdot 7^2\cdot 11\cdot 13}{5^{10}}>\frac{2^3\cdot 3^5\cdot 7^2\cdot 10\cdot 12}{5^{10}}=\frac{2^6\cdot 3^6 \cdot 7^2}{5^9}$$

Again carefully we replace $7\cdot 3 > 20$

$$\frac{2^6\cdot 3^6 \cdot 7^2}{5^9}>\frac{2^6\cdot 3^4\cdot 20^2}{5^9}=\frac{2^{10}\cdot 3^4}{5^7}$$

Again we have $2^{10}$

$$\frac{2^{10}\cdot 3^4}{5^7}>\frac{1000\cdot 3^4}{5^7}=\frac{2^3\cdot 3^4}{5^4}$$

I think we can handle this now

$$\frac{2^3\cdot 3^4}{5^4}=\frac{648}{625} > 1$$

And this is what we wanted to prove.

All along we have used the fact that these two values are very much away from each other.

Answer 5

Using Ross Millikan's suggestion and Ivoirians's idea, let us consider $$f(n)=\log_{100}(n!)-n$$ Now, let us use Stirling approximation for $n!$; this gives $$f(n) =-n+\frac{n (\log (n)-1)}{\log (100)}+\frac{\log (2 \pi n)}{2 \log (100)}+O\left(\sqrt{\frac{1}{n}}\right)$$ So, $$f'(n)\approx \frac{\log (n)}{\log (100)}+\frac{1}{n \log (10000)}-1$$ $$f''(n)\approx \frac{1}{n \log (100)}-\frac{1}{n^2 \log (10000)}$$ The second derivative is positive for any value of $n>1$.

The first derivative cancels at $$n_*=100 e^{W\left(-\frac{1}{200}\right)}$$ where appears Lambert function which can be approximated again; so $n_*\approx 99.5$ which corresponds to a minimum of $f(n)$. Now, a look at the function $f(n)$ shows that it is negative for $n<268$ and positive for any larger value of the argument.

Edit

May be, you could be interested by this question of mine which, adapted to your problem, shows that an upper bound ot the solution of $n!=a^n$ is given by $$n=-\frac{\log (2 \pi )}{2 W\left(-\frac{\log (2 \pi )}{2 e a}\right)}$$ which, for large values of $a$, can be approximated by $n\approx e a-\frac{1}{2} \log (2 \pi ) $. For $a=100$, this leads to $n \approx 271$.

Answer 6

According to Mathematica :

$300!=$306057512216440636035370461297268629388588804173576999416776741259476533176716867465515291422477573349939147888701726368864263907759003154226842927906974559841225476930271954604008012215776252176854255965356903506788725264321896264299365204576448830388909753943489625436053225980776521270822437639449120128678675368305712293681943649956460498166450227716500185176546469340112226034729724066333258583506870150169794168850353752137554910289126407157154830282284937952636580145235233156936482233436799254594095276820608062232812387383880817049600000000000000000000000000000000000000000000000000000000000000000000000000

$100^{300}=$1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000

therefore $300!\geq 100^{300}$ ($300!/100^{300}\approx 3\times10^{14}$).

Plotting $\Gamma(n)/100^n$ tells us that the inequality is true for $n\geq 274$ :

Answer 7

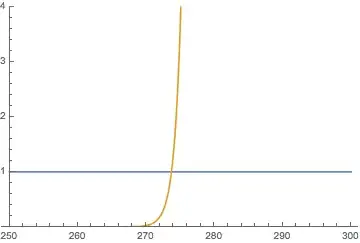
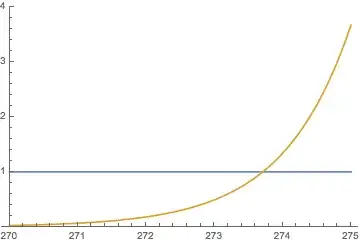
Consider $$k! > n^k$$ and note that $$\lim_{k\to \infty} \frac{(k!)^{1/k}}{k} = \frac{1}{e}$$

This implies that if $n$ is smaller than $\frac{k}{e}$, the first statement is true. So if we take $n = 100$ and $k = 300$, we get

$$100 < \frac{300}{e}$$

and $$300! > 100^{300}$$