5

Given the following sequence $d(n) = x \cdot n - \lfloor x \cdot n \rfloor$ with $n \in \mathbb{N}$, $x \in \mathbb{R} \backslash \mathbb{Q}$ .

I want to show that for every $z \in [0,1)$ there is a subsequence of $d(n)$ that converges against $z$.

Notes:

I am having serious problems of finding such a subsequence, first I see what the sequence does. If you take for example the subsequence $a(n) = d(10^n)$ you see that it gives you the decimal representation of $x$ starting with the $n'th$ digit. Example: let $x=\pi$, then we get $a(0)=0.141592..., a(1)=0.41592..., a(2)=0.1592...$ and so on.

Also this is a plot of $d(n)$ for $x=\pi$:

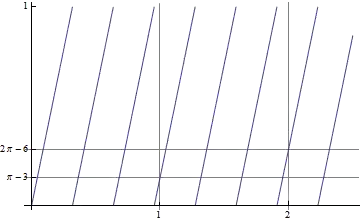
Plot of d(n)

You see that for irrational x the height of the function at integers is not constant, nor periodic.

Also this question I asked several weeks ago seems to be related: Proving that an equation is solvable, Floor function

Community
  • 1
Listing
  • 13,937

1 Answers1

1

If I have understood your question correctly, I believe this follows from the Equidistribution theorem. For more info refer: Equidistributed Sequence.

Aryabhata
  • 82,206
  • Thank you for your answer. Yes you are right but I think the fact that it is uniformly distributed is stronger than what I want to show. I hope that there is a simpler proof that can live without integrals :-) – Listing Jan 02 '11 at 22:30
  • @user3123: No idea if a simpler proof exists. Where did you get this problem? – Aryabhata Jan 03 '11 at 06:15
  • Our Analysis Teacher gave us a holiday sheet we could make if we wanted and this has prooved to be the only tough question on it. I investigated a bit further and found this -> http://at.yorku.ca/cgi-bin/bbqa?forum=ask_an_analyst_2005;task=show_msg;msg=2719.0001.0001.0001 on a forum about topology. I guess it uses http://math.stackexchange.com/questions/10280/proving-that-an-equation-is-solvable-floor-function to show that there is a sequence that has a limit in every open interval. Then you could choose a interval of length $2^{-n}$ to prove it i think? But I don't fully understand it – Listing Jan 03 '11 at 10:47
  • @user: That works, if a set A is dense in an interval, then for even real number r in that interval, there is a sequence of elements of A which converges to r. Remember the proof that for every real number there is a sequence of rationals converging to it? – Aryabhata Jan 03 '11 at 17:14