how to calculate $\int_{0}^{\infty}\frac{x}{\sqrt{e^x-1}}\mathrm{d}x$

Question

I was trying to solve another integral when then I reached this, I've no idea of how to select the contour for the integration.

Answer 1

Let $t^2= e^x-1$. We have $$2tdt = e^xdx = (1+t^2)dx \implies dx = \dfrac{2tdt}{1+t^2}$$ Hence, we have $$I = \int_0^{\infty} \dfrac{xdx}{\sqrt{e^x-1}} = \int_0^{\infty} \dfrac{2t \log(1+t^2)dt}{(1+t^2)t} = 2\int_0^{\infty} \dfrac{\log(1+t^2)}{(1+t^2)}dt$$ Let $$I(a) = \int_0^{\infty} \dfrac{\log(1+a^2t^2)}{1+t^2}dt \,\,\, (\clubsuit)$$ We need $2I(1)$. Differentiating $(\clubsuit)$, we obtain $$I'(a) = \int_0^{\infty} \dfrac{2at^2}{(1+a^2t^2)(1+t^2)}dt = \dfrac{2a}{a^2-1}\left(\int_0^{\infty} \dfrac{dt}{1+t^2} - \int_0^{\infty} \dfrac{dt}{1+a^2t^2} \right)$$ Hence, $$I'(a) = \dfrac{2a}{a^2-1}\left(\dfrac{\pi}2 - \dfrac{\pi}{2a}\right) = \dfrac{\pi}{(1+a)} \,\,\, (\spadesuit)$$ Further, we have $I(0) = 0$. Hence, integrating $(\spadesuit)$, we obtain $$I(a) = \pi \log(1+a)$$ The desired integral is $2I(1) = \pi \log(2)$.

Answer 2

Sub $x=\log{(1+y^2)}$; then the integral is equal to

$$\int_{-\infty}^{\infty} dy \frac{\log{(1+y^2)}}{1+y^2} $$

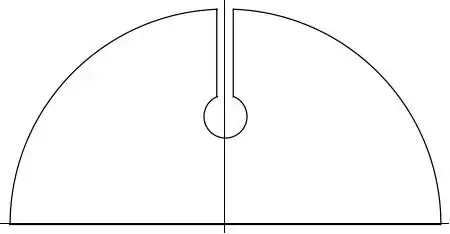
I will illustrate how to use complex analysis to evaluate this integral. Consider the following contour integral:

$$\oint_C dz \frac{\log{(1+z^2)}}{1+z^2} $$

where $C$ is the following contour:

i.e., a semicircular contour of radius $R$ with a detour around the branch point at $z=i$ of radius $\epsilon$. The contour integral is equal to

$$\int_{-R}^R dx \frac{\log{(1+x^2)}}{1+x^2} + i R \int_0^{\pi/2} d\theta \, e^{i \theta} \frac{\log{(1+R^2 e^{i 2 \theta})}}{1+R^2 e^{i 2 \theta}} \\ + i \int_R^{1+\epsilon} dy \frac{\log{(y^2-1)}+i \pi}{1-y^2} + i \epsilon \int_{\pi/2}^{-3 \pi/2} d\phi \, e^{i \phi} \frac{\log{[1+(i+\epsilon e^{i \phi})^2]}}{1+(i+\epsilon e^{i \phi})^2} \\ + i \int_{1+\epsilon}^R dy \frac{\log{(y^2-1)}-i \pi}{1-y^2} + i R \int_{\pi/2}^{\pi} d\theta \, e^{i \theta} \frac{\log{(1+R^2 e^{i 2 \theta})}}{1+R^2 e^{i 2 \theta}}$$

Note that the third and fifth integrals are on opposite sides of the branch cut along the imaginary axis above $z=i$. Also note the limits on the fourth integral: the upper limit is less than the lower limit because the contour traverses clockwise locally about the branch point $z=i$.

We consider the limits as $R \to \infty$ and $\epsilon \to 0$. In these limits, the second and sixth integrals vanish. Rearranging things a bit, we get for the contour integral

$$\int_{-\infty}^{\infty} dx \frac{\log{(1+x^2)}}{1+x^2} - i (-i 2 \pi) \int_{1+\epsilon}^{\infty} \frac{dy}{y^2-1} + \frac12 \int_{\pi/2}^{-3 \pi/2} d\phi \, \left [\log{(i 2 \epsilon)} + i \phi \right ] $$

Note that, while there appears to be singular behavior as $\epsilon \to 0$, that singular behavior will cancel out as we will see.

By Cauchy's theorem, the contour integral is zero. Doing out the second and third integrals, we find that

$$\int_{-\infty}^{\infty} dx \frac{\log{(1+x^2)}}{1+x^2} - \pi \left [\log{\left (\frac{y-1}{y+1} \right )} \right ]_{1+\epsilon}^{\infty} - \pi \log{(i 2 \epsilon)} + i \frac14 (2 \pi^2) = 0$$

Simplifying, and taking $\log{i} = i \pi/2$, we get

$$\int_{-\infty}^{\infty} dx \frac{\log{(1+x^2)}}{1+x^2} + \pi \log{\epsilon} - \pi \log{2} - i \frac{\pi^2}{2} - \pi \log{2} - \pi \log{\epsilon} + i \frac{\pi^2}{2} = 0$$

Thus...

$$\int_0^{\infty} dx \frac{x}{\sqrt{e^x-1}} = 2 \pi \log{2} $$

Answer 3

Let $z=\mathrm{e}^{x}-1$, so that we have \begin{equation} \int\limits_{0}^{\infty} \frac{\mathrm{ln}(z+1)}{\sqrt{z}}\frac{1}{z+1} \mathrm{d} z \end{equation}

Let us consider \begin{equation} I(a) = \int\limits_{0}^{\infty} \frac{(z+1)^{a}}{\sqrt{z}} \mathrm{d} z = \mathrm{B}\left(\frac{1}{2}, -\frac{1}{2}-a\right) = \frac{\Gamma\left(\frac{1}{2}\right) \Gamma\left(-\frac{1}{2}-a\right)}{\Gamma(-a)} \end{equation} so that \begin{equation} \lim_{a \to -1} \frac{\partial I(a)}{\partial a} = \int\limits_{0}^{\infty} \frac{\mathrm{ln}(z+1)}{\sqrt{z}}\frac{1}{z+1} \mathrm{d} z = \int\limits_{0}^{\infty} \frac{x}{\sqrt{\mathrm{e}^{x}-1}} \mathrm{d} x \end{equation}

Then, \begin{equation} \frac{\partial I(a)}{\partial a} = \Gamma\left(\frac{1}{2}\right)\left[\frac{-\Gamma(-a)\Gamma\left(-\frac{1}{2}-a\right)\psi^{0}\left(-\frac{1}{2}-a\right) + \Gamma\left(-\frac{1}{2}-a\right)\Gamma(-a)\psi^{0}(-a)}{\Gamma(-a)\Gamma(-a)} \right] \end{equation}

\begin{align} \lim_{a \to -1} \frac{\partial I(a)}{\partial a} & = -\frac{\Gamma\left(\frac{1}{2}\right)\Gamma\left(\frac{1}{2}\right)}{\Gamma(1)} \left[\psi^{0}\left(\frac{1}{2}\right) - \psi^{0}(1)\right] \\ & = -\pi[(-\gamma-\mathrm{ln}4) -(- \gamma)] \\ & = \pi\mathrm{ln}4 \\ & = \int\limits_{0}^{\infty} \frac{x}{\sqrt{\mathrm{e}^{x}-1}} \mathrm{d} x \end{align}

Answer 4

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{\displaystyle{#1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\mc}[1]{\mathcal{#1}} \newcommand{\mrm}[1]{\mathrm{#1}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ With $\ds{t \equiv \expo{x} - 1 \implies x = \ln\pars{1 + t}}$: \begin{align} &\bbox[5px,#ffd]{\int_{0}^{\infty} {x \over \root{\expo{x} - 1}}\,\dd x} = \int_{0}^{\infty} t^{-1/2}\,\,\,{\ln\pars{1 + t} \over 1 + t}\,\dd t \\[5mm] = &\ \int_{0}^{\infty} t^{\color{red}{1/2} - 1}\bracks{% -\sum_{k = 0}^{\infty}H_{k}\,\pars{-t}^{k}}\,\dd t \\[5mm] = &\ -\int_{0}^{\infty} t^{\color{red}{1/2} - 1} \bracks{% \sum_{k = 0}^{\infty} \color{red}{H_{k}\,\Gamma\pars{1 + k}} {\pars{-t}^{k} \over k!}}\dd t \end{align} With the Ramanujan's Master Theorem: \begin{align} &\bbox[5px,#ffd]{\int_{0}^{\infty} {x \over \root{\expo{x} - 1}}\,\dd x} \\[5mm] = &\ -\ \underbrace{\Gamma\pars{\color{red}{1 \over 2}}} _{\ds{\root{\pi}}}\ \underbrace{\quad H_{\color{red}{-1/2}}\quad} _{\ds{\int_{0}^{1}{1- t^{\color{red}{-1/2}} \over 1 - t} \,\dd t}}\ \Gamma\pars{1 \color{red}{- {1 \over 2}}} \\[5mm] = &\ -\pi\int_{0}^{1}{1- t^{-1} \over 1 - t^{2}}\,2t\,\dd t = 2\pi\int_{0}^{1}{\dd t \over 1 + t} \\[5mm] = &\ \bbx{2\pi\ln\pars{2}} \approx 4.3552 \\ & \end{align}