1

If I intersect a ball with a plane, then I can see how to make sense of the radius of the resulting circle of intersection. But if the circle lies strictly on the surface of the ball (sphere), then how do I make sense of the radius of such circle, since it won't be half the length of a straight line anymore? Will it be an arc-length?

Thanks!

user210190
  • 147
  • What do you mean by a circle lying on the surface of the sphere as opposed to one formed by the intersection of the sphere and a plane? – Jeffrey Jan 13 '16 at 03:19
  • May be think of someone drawing a circle on the surface of a bowling ball...? The radius of that circle. – user210190 Jan 13 '16 at 03:21
  • I think the asker wants to calculate the radius with the intrinsic metric of the sphere. – Samuel Coskey Jan 13 '16 at 03:24
  • I think one needs to use Riemannian geometry.. – Meow Jan 13 '16 at 03:31
  • https://en.wikipedia.org/wiki/Circle_of_a_sphere may be this will help – Meow Jan 13 '16 at 03:36
  • Thanks, I guess the radius would have to be the length of an arc and not the length of a straight line. – user210190 Jan 13 '16 at 03:53
  • if I draw a circle on the surface of a sphere, e.g. the earth with a $100km$ compass, why and how will that circle be a real circle, given that I'm an earthling which is drawing on a curved riemannian manifold ? – reuns Jan 13 '16 at 03:54
  • In the absence of additional context, I'd go with "the Euclidean radius", i.e., the same radius as the disk of intersection between the ball and plane. – Andrew D. Hwang Jan 13 '16 at 03:54
  • If you're talking about drawing circles on a sphere with a fixed center on the sphere, that constitutes "additional context". In that case, I'd go with "arc length measured along the surface of the sphere". – Andrew D. Hwang Jan 13 '16 at 03:56
  • Thanks Andrew, that's what I thought the radius would be. – user210190 Jan 14 '16 at 03:45

2 Answers2

1

A circle that you simply draw on the surface of a ball is just like a circle that you make by intersecting a plane with a ball, which is just like a circle you draw with a compass on a plane, assuming this is all done in three-dimensional Euclidean space.

Each of these is a closed path in space with certain properties of curvature. You can always construct the plane in which the circle lies, even if that plane is not how you defined the circle. You can even construct any of an infinite number of balls whose surfaces happen to contain the circle, if you want to.

In either of the situations you described, you have a particular ball you are concerned with, so we don't have to be concerned with all possible balls, just this one. But there is always a plane containing the circle, and the diameter of the circle in that plane is a straight line.

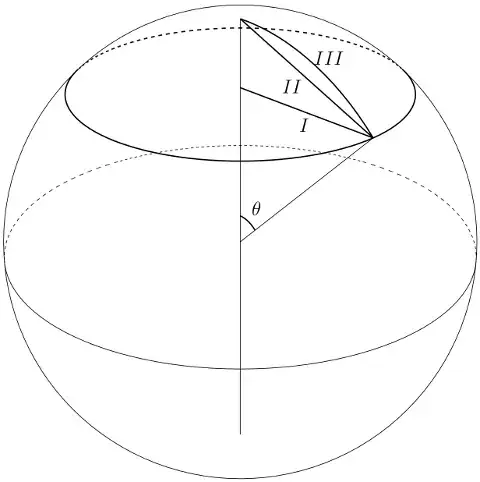
What you do need to think about is how you want to use the radius. If the circle is mainly interesting because it is the outer boundary of the set of all points you can reach by traveling a certain distance from a certain point $P$ on the sphere, then the relevant measurement is the length of the shortest path on the sphere from $P$ to one of the points on the circle. I would consider this to be the radius of the circle measured on the surface of the ball. But if you want to know the circumference of the circle, or if you want to write a vector expression parameterizing the circle, the planar radius of the circle (measured along a straight line in the plane of the circle) might be more useful.

David K
  • 98,388
0

$\newcommand{\Reals}{\mathbf{R}}$Let $S$ be a sphere of radius $R$ in $\Reals^{3}$, and let $C$ be a circle on $S$ subtending an angle $\theta$ (with $0 < \theta < \pi$), as shown. There are at least three senses in which $C$ has a "radius" $r$. Each interpretation arises naturally in non-trivial settings.

Three notions of radius of a circle on a sphere

  • The Euclidean radius, with the circle's center in the Euclidean plane containing the circle ($I$ in the diagram). $r = R\sin\theta$; the circumference of $C$ is $2\pi r$.

  • The Euclidean radius, with the circle's center on the sphere ($II$ in the diagram). $r = 2R\sin(\theta/2)$; the area of the disk enclosed by $C$ is $\pi r^{2}$. (!!)

  • The arc of the sphere, with the circle's center on the sphere ($III$ in the diagram). $r = R\theta$ is the intrinsic radius, referring only to measurements in the sphere.

(Each of the last two is a double interpretation, since a circle on a sphere has two antipodal centers.)

The bottom line for "What is the radius of $C$?" is "It depends on context."

Community
  • 1
Andrew D. Hwang
  • 78,195