How to get $ \cot(\theta/2)$ from $ \frac {\sin \theta} {1 - \cos \theta} $?

Question

According to wolfram alpha, $\dfrac {\sin \theta} {1 - \cos \theta} = \cot \left(\dfrac{\theta}{2} \right)$.

But how would you get to $\cot \left(\dfrac{\theta}{2} \right)$ if you're given $\dfrac {\sin \theta} {1 - \cos \theta}$?

Answer 1

Proof without words: $\displaystyle\cot(\theta/2)=\frac{\color{green}{\sin(\theta)}}{\color{red}{1-\cos(\theta)}}$

$\hspace{3.5cm}$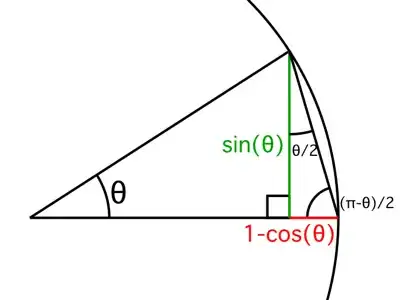

Answer 2

All you need are the following formulas:

$$\sin(2A) = 2 \sin(A) \cos(A) \text{ and } \cos(2A) = 1 - 2 \sin^2(A)$$ Now take $A = \theta/2$ to get that $$\sin(\theta) = 2 \sin(\theta/2) \cos(\theta/2) \text{ and } \cos(\theta) = 1 - 2 \sin^2(\theta/2)$$ Now plugging this into your equation, we get that $$\dfrac{\sin(\theta)}{1-\cos(\theta)} = \dfrac{2 \sin(\theta/2) \cos(\theta/2)}{2 \sin^2(\theta/2)} = \dfrac{\cos(\theta/2)}{\sin(\theta/2)} = \cot(\theta/2)$$

Answer 3

Alternately, use these formulas: $$\cos(\theta)=\frac{e^{i\theta}+e^{-i\theta}}{2} \mbox{and} \, \sin(\theta)=\frac{e^{i\theta}-e^{-i\theta}}{2i} \, .$$

So \begin{eqnarray*} \frac{\sin(\theta)}{1-\cos(\theta)} & = & \frac{(e^{i \theta} - e^{-i \theta})/(2i)}{(2-e^{i \theta}-e^{-i\theta})/2}\\ & = & \frac{1}{i}\frac{(e^{i \theta/2} +e^{-i\theta/2})(e^{i\theta/2}-e^{-i\theta/2})}{-(e^{i \theta/2}-e^{-i\theta/2})^2}\\ & = & i\frac{e^{i \theta/2}+e^{-i\theta/2}}{e^{i\theta/2}-e^{-i\theta/2}}\\ & =& i \frac{2\cos (\theta/2)}{2i \sin (\theta/2)}\\ & =& \cot(\theta/2) \, .\end{eqnarray*}

Answer 4

There is a very standard way of transforming trigonometric functions into rational functions of a different variable - generally first learned when integrating functions, but heavily related to the unit circle and illustrative of basic concepts in algebraic geometry.

One sets $t=\tan \frac \theta 2$, when $\sin \theta = \frac {2t} {1+t^2} $ and $\cos \theta = \frac {1-t^2}{1+t^2}$

This gives the result easily, and is worth knowing.

Answer 5

It may not seem obvious at first, but substitute $\theta = 2\varphi$ first because we want to work with integer multiples of the angle rather than fractional multiples.

$$\begin{array}{rcl} \dfrac{\sin \theta}{1 - \cos \theta} &=& \dfrac{\sin 2\varphi}{1 - \cos 2\varphi} \end{array}$$ Then we use double angle formula. $$\begin{array}{rcl}\dfrac{\sin \theta}{1 - \cos \theta} &=& \dfrac{2\sin \varphi\cos\varphi}{1-\left(1-2\sin^2 \varphi\right)}\\ &=& \dfrac{2\sin\varphi\cos\varphi}{2\sin^2\varphi}\\ &=& \dfrac{\color{blue}{2\sin \varphi} \cos \varphi}{\color{blue}{2\sin\varphi} \sin \varphi}\\ &=& \dfrac{\cos \varphi}{\sin\varphi}\\ &=& \cot \varphi \end{array}$$ Recall that $\theta = 2\varphi$, so dividing by 2 on both sides gives $\varphi = \dfrac{\theta}{2}$.

We can conclude that $$\begin{array}{rcl}\dfrac{\sin \theta}{1 - \cos\theta} &=& \cot \varphi\\ &=& \boxed{\cot \left(\dfrac{\theta}{2}\right)} \end{array}$$