probability density of the maximum of samples from a normalized uniform distribution

Question

Suppose

$$X_1, X_2, \dots, X_n\sim Unif(0, 1), iid$$

and suppose

$$\hat\theta = \max\{X_1, X_2, \dots, X_n\} / \sum_i^nX_i$$

How would I find the probability density of $\hat\theta$?

I know the answer if it's iid. But I don't know how to formalize the fact that the sum is iqual to 1.

a simiar question can be found here: probability density of the maximum of samples from a uniform distribution

---

I arrive here: \begin{align} P(Y\leq x)&=P(\max(X_1,X_2 ,\cdots,X_n)/\sum_i^nX_i\leq x)\\&=P(X_1/\sum_i^nX_i\leq x,X_2/\sum_i^nX_i\leq x,\cdots,X_n/\sum_i^nX_i\leq x)\\ &\stackrel{ind}{=} \prod_{j=1}^nP(X_j/\sum_i^nX_i\leq x )\\& \ \ \ \ \ \end{align}

Answer 1

Note that $$\hat\theta_n\sim \frac 1 {1+\sum_{i=1}^{n-1}U_i} $$ for i.i.d. standard uniforms $U_i$. Now see this and this

Answer 2

If this is any help, here are some simulations of the density.

Answer 3

Because of symmetry, it is sufficient to only look at the cases where $X_1$ is the maximum. In that case, $X_2, \dots, X_n$ are independent and uniformly distributed between 0 and $X_1$. $$\theta = \frac{X_1}{X_1 + \sum_{i=2}^n X_i} \quad \text{with} \ X_2, \dots, X_n \sim U(0, X_1)$$ Now we divide by $X_1$ on both sides of the fraction and we get the formula A.S. gave us. $$\theta = \frac{1}{1 + \sum_{i=2}^n X_i} \quad \text{with} \ X_2, \dots, X_n \sim U(0, 1)$$ The sum of $n$ iid standard uniform random variables has the Irwin–Hall distribution. It's PDF (probability density function) is: $$f(x) = \frac{1}{2\left(n-1\right)!}\sum_{k=0}^n\left(-1\right)^k{n \choose k}\left(x-k\right)^{n-1}\operatorname{sgn}(x-k)$$ Let $$ X = \sum_{i=2}^n X_i $$ The PDF of $X$ is: $$f_X(x) = \frac{1}{2\left(n-2\right)!}\sum_{k=0}^{n-1}\left(-1\right)^k{n-1 \choose k}\left(x-k\right)^{n-2}\operatorname{sgn}(x-k)$$ Now we can use change of variable to calculate the PDF of $\theta$. The following formula gives the PDF of $\theta$ if $\theta = g(X)$ and $g(x)$ is monotonic.

$$f_\theta(y) = \left| \frac{\mathrm{d}}{\mathrm{d}y} (g^{-1}(y)) \right| \cdot f_X(g^{-1}(y))$$ We have $$ \begin{array}{rl} g(x) &= \frac{1}{1 + x} \\ g^{-1}(y) &= 1/y - 1 \\ \left| \frac{\mathrm{d}}{\mathrm{d}y} g^{-1}(y) \right| &= y^{-2} \end{array} $$ So the PDF of $\theta$ is: $$ \begin{array}{rl} f_\theta(y) &= \displaystyle \frac{1}{2 y^2 \left(n-2\right)!}\sum_{k=0}^{n-1}\left(-1\right)^k{n-1 \choose k}\left(1/y-1-k\right)^{n-2}\operatorname{sgn}(1/y-1-k) \\ &= \displaystyle \frac{-1}{2 y^2 \left(n-2\right)!}\sum_{k=1}^{n}\left(-1\right)^k{n-1 \choose k-1}\left(1/y-k\right)^{n-2}\operatorname{sgn}(1/y-k) \end{array} $$ It is positive at $y \in (1/n, 1)$.

Approximation for large $n$

The mean and the variance of the Irwin-Hall distribution are respectively $\mu=n/2$ and $\sigma^2=n/12$. Because the Irwin-Hall distribution is the sum of $n$ iid random variables, the central limit theorem states that for large $n$ its distribution is very close to the normal distribution with the same mean and variance. The normal distribution has PDF: $$f(x) = \frac{1}{\sigma\sqrt{2\pi} } \; \exp\left( -\frac{(x-\mu)^2}{2\sigma^2} \right)$$ Replacing $\mu$ and $\sigma^2$ with the mean and variance of the Irwin-Hall distribution with parameter $n-1$ gets us: $$f_X(x) \approx \frac{1}{\sqrt{\pi (n-1)/6} } \; \exp\left( -\frac{(x-(n-1)/2)^2}{(n-1)/6} \right)$$ Using the same change of variable technique as above, we get the distribution of $\theta$ for large $n$: $$ \begin{array}{rl} f_\theta(y) &\approx \displaystyle \frac{1}{y^2\sqrt{\pi (n-1)/6} } \; \exp\left( -\frac{(1/y-1-(n-1)/2)^2}{(n-1)/6} \right) \\ &= \displaystyle \frac{1}{y^2\sqrt{\pi (n-1)/6} } \; \exp\left( -\frac{3}{2}\cdot\frac{(2/y-n-1)^2}{n-1} \right) \end{array} $$

Answer 4

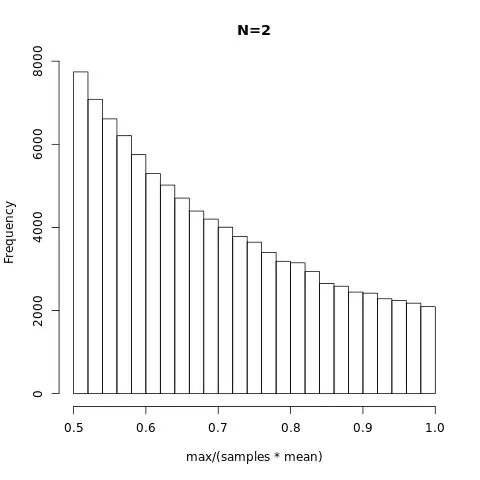
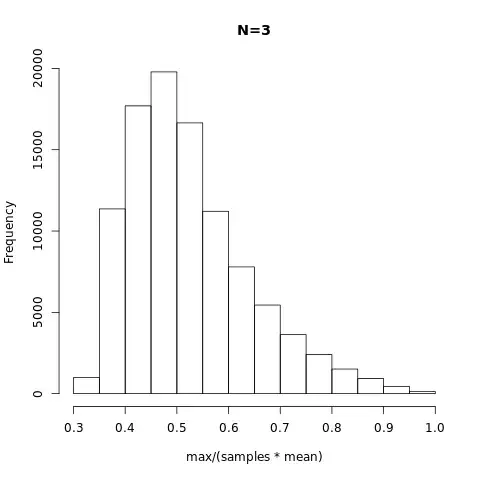
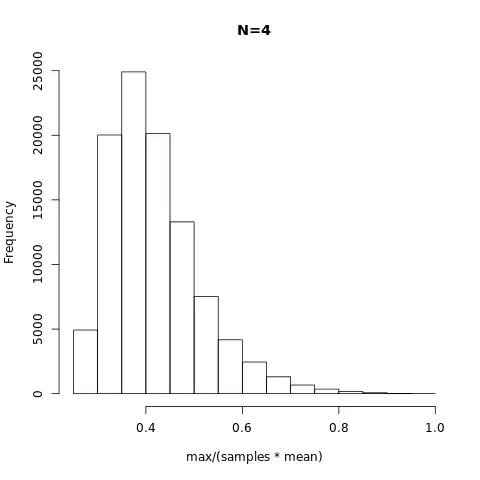
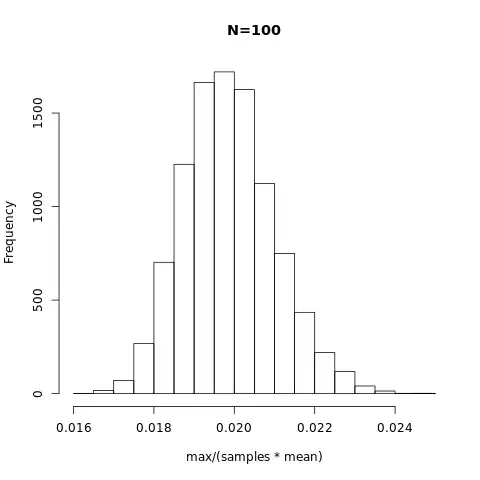
Let me first rephrase the problem a little bit

$$ P(\theta)d\theta = \left[\int_{0}^1 dy P(\max\{X_i\}=y)\cdot P\left(\bar{X}=\frac{y}{n\theta} \middle| \max \{X_i\}=y \right)\right]d\bar{X} $$

It is mentioned in this link that $$ P(\max\{X_i\}=y)=y^n $$

Without losing generosity, I can also reorder the ${X_i}$ to be ${\mu_i}$,so that $\mu_n=\max\{X_i\}=y$.

Now I can define $\bar{\mu}=\sum_{i=0}^{n-1}\mu_i/(n-1)$ , thus $$ P\left(\bar{X}=\frac{y}{n\theta} \middle| \max \{X_i\}=y \right)d\bar{X} = P\left(\bar{\mu}=\frac{1-\theta}{(n-1)\theta}y \middle| \mu_i \sim Unif(0,y)\right)d\bar{\mu} $$

Further define $z_i=y\mu_i$, we can write

$$ P(\theta)d\theta = \int_{0}^1 dy d\bar{\mu} \left[ y^n\cdot P\left(\bar{\mu}=\frac{1-\theta}{(n-1)\theta}y \middle| \mu_i \sim Unif(0,y) \right)\right] \\ = \int_{0}^1 dy \underbrace{ d\bar{z} \left[P\left(\bar{z}=\frac{1-\theta}{(n-1)\theta}y \middle| z_i \sim Unif(0,1) \right)\right] }_{P_0} $$

Notice the part I labeled as $P_0$ is independent of $y$, so we can carry out the integral trivially. $$ P(\theta)d\theta = P_0= \left[P\left(\bar{z}=\frac{1-\theta}{(n-1)\theta}y \middle| z_i \sim Unif(0,1) \right)\right] d\bar{z} \\ =\left[P\left(\bar{z}=\frac{1-\theta}{(n-1)\theta}y \middle| z_i \sim Unif(0,1) \right)\right] \left|\frac{1}{(n-1)\theta^2}\right|d\theta $$

I believe there is some general analytic form for this distribution of $\bar{z}$ for arbitrary $n$, but I just can't solve that. However, there are some solvable examples to test this formula:

n=2: $$ P(\theta)=\left[P\left(z_1=\frac{1-\theta}{\theta} \middle| z_1 \sim Unif(0,1) \right)\right] \frac{1}{\theta^2} = \frac{1}{\theta^2} $$

n=3: $$ P(\theta)=\left[P\left(\frac{z_1+z_2}{2}=\frac{1-\theta}{2\theta} \middle| z_1,z_2 \sim Unif(0,1) \right)\right] \frac{1}{2\theta^2} =\left[2-4*\left|\frac{1-\theta}{2\theta}-0.5\right|\right] \frac{1}{2\theta^2} $$

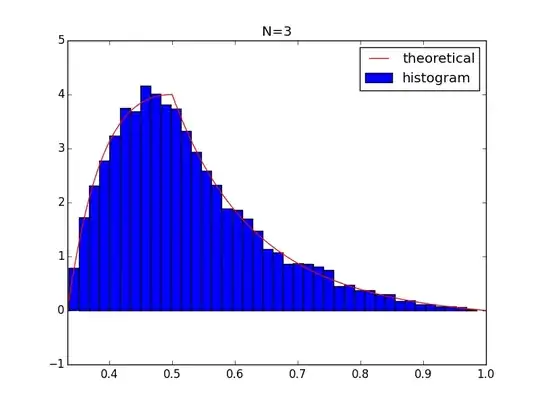
n is large

When $n$ is large, from central limit theorem, we know that $$ P\left(\bar{z}=\frac{1-\theta}{(n-1)\theta} \middle| z_i \sim Unif(0,1) \right) \approx P_\text{Gauss}\left(\frac{1-\theta}{(n-1)\theta}, \mu=0.5, \sigma^2=\frac{1}{12n}\right)\\ =\sqrt{\frac{6n}{\pi}}\exp\left[-6n\left(\frac{1-\theta}{(n-1)\theta}-0.5\right)^2\right] $$

With some approximation $n\gg 1$, we can write down the form more neatly as $$ \lim_{n\to \infty}P(\theta)\approx \frac{1}{n\theta^2} \sqrt{\frac{6n}{\pi}}\exp\left[-6n\left(\frac{1-\theta}{n\theta}-0.5\right)^2\right] $$

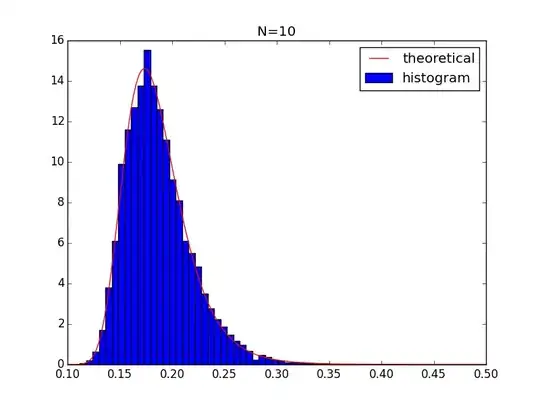
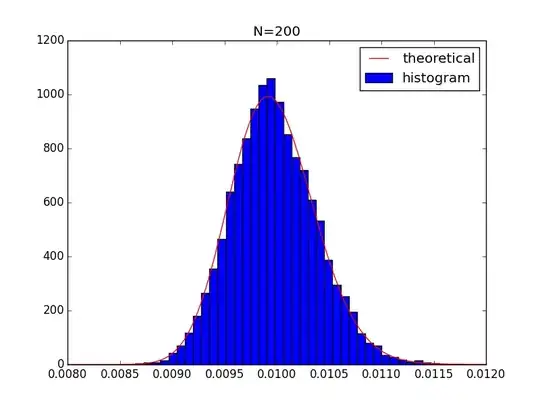
MLE with large n The value of maximum probability density is approximately $$ \frac{1-\theta}{n\theta}=0.5 \Rightarrow \theta=\frac{2}{n} $$