Double Integral using riemann sums

Question

So there is $R=\left[-1,3\right]\times\left[0,2\right]$. I have to use a Riemann sum with m=4,n=2 to estimate the value of double integral $\int \int(y^2-2x^2)\ \mathrm{d}A$, taking the sample points to be the upper left corners of the rectangles. So I evaluated it and got $-4$ but can Riemann sum of a double integral be negative? Taking the double integral over a rectangle should equal to the volume of the solid between the function and the rectangle and I don't think volumes can be negative?

There is nothing wrong with the integral being negative. It just means on average the integrand is negative. — Paul, Jan 10 '16 at 23:00
Oh it doesn't? I thought volumes always have to be positive? — Jermaine Law, Jan 10 '16 at 23:13
Volumes, yes. This is not exactly the same as a volume, since you are integrating over something that is both positive and negative. — Paul, Jan 10 '16 at 23:26

score 1 · Accepted Answer · answered Jan 10 '16 at 23:28

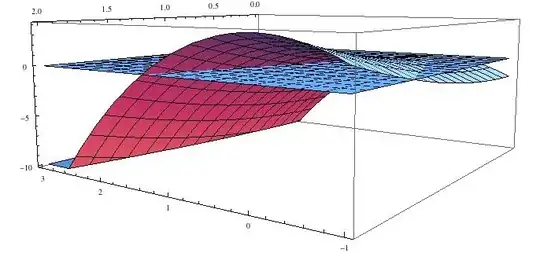
Here is a graph of $y^2 - 2x^2$ and the plane $z=0$.

From the plot, you can see that most of the function lies below z=0, So the integral = -4 makes good sense.

If you were to interpret the integral as the volume between the function and the rectangle, make sure your function is non-negative over the rectangle. I think that where your getting hung up.

Double Integral using riemann sums

1 Answers1