16

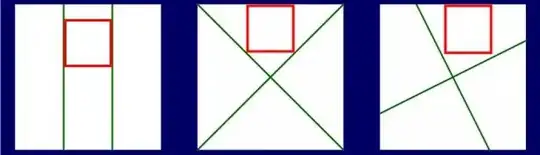
I found this problem on Keith Ball's blog sometime ago but I've never really worked it out.

enter image description here

Show that if a square is cut by two lines (shown above in green) then there is an uncut square at least one third as large (shown in red) lying inside the original (and aligned with it).

If this is too easy, try it with three lines and an uncut square at least one quarter as large as the original.

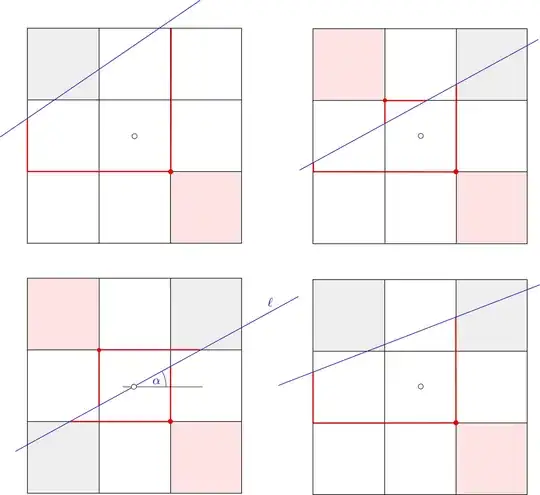
My first intuition was to use pigeonhole principle on a $3\times 3$ grid of equally sized squares, but one can clearly choose a sort of diagonal line passing through five squares. I don't think arguing by cases is particularly elegant and it may not be the inspired solution to the problem. Could anyone help?

E.Lim
  • 1,185
  • You mean cut into pieces of same size, don't you? – adjan Jan 10 '16 at 11:10
  • @addy2012 Not necessarily, I think. – Adhvaitha Jan 10 '16 at 11:11
  • 2
    @Leg okay. these images were just so suggestive :) – adjan Jan 10 '16 at 11:12
  • 1
    @addy2012 But I would like to believe that equal areas of each piece would be sort of the worst case. – Adhvaitha Jan 10 '16 at 11:12
  • I mean, this is a special case of the "geometric pigeonhole principle" he describes as a corollary to the real planck principle in the DIscrete Geometry section here: https://keithmball.wordpress.com/current-research-interests/ Surely there's a more direct approach that he intended for this problem. – Dan Jan 14 '16 at 19:27

1 Answers1

13

Let the large square have side length $3$. Note that in the figures of the OP appear two completely different limiting cases where no small square with side length $>1$ can be placed. Any proof will have to incorporate these cases somehow.

If there are no cutting lines we can move a small (unit) square along the inner boundary of the large square along a track of total length $8$. We shall show that a single cutting line $\ell$ leaves a part of length $\geq4$ of this track available for the small square. It follows that two cutting lines cannot make all points of the track unavailable.

enter image description here

Place the large square with its center at the origin. By symmetry, it is enough to consider cutting lines $\ell$ given by an equation of the form $y=\tan\alpha \cdot x+c$ with $0\leq\alpha\leq{\pi\over4}$ and $c\geq0$. Such a line $\ell$ will cut $n\in\{0,1,2\}$ little corner squares (shaded grey in the above figures). The case $n=0$ is not drawn; the upper two figures show the case $n=1$, and the lower two figures show the case $n=2$. It is easily verified that in each case the pink squares can move freely along a total track length $\geq4$.

Christian Blatter
  • 226,825