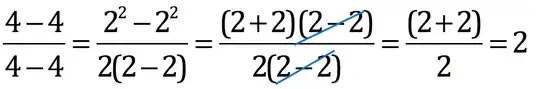2

I can't find where the mistake is here. Can someone explain how it is possible?

enter image description here

Paul
  • 8,153
Hax
  • 89
  • 3
    0/0 is called indefinite form. It can be equal to anything. – Jimmy R. Jan 09 '16 at 23:26
  • To expand on the previous comment, if $b=\frac{0}{0}$, then $b$ satisfies $b*0 = 0$. But every number has this property, hence $\frac{0}{0}$ is indeterminate. Note that the fraction is undefined since a unique value cannot be ascribed to it. – MathematicsStudent1122 Jan 09 '16 at 23:42
  • If you're going to cancel like terms, then you might as well just cancel $4-4$ from the start, giving $1$ (which is fallacious for the same reason). – Théophile Jan 10 '16 at 00:10
  • 2
    Learn this now: You can not divide by zero. EVER. 4-4/4-4 is undefined ... because you can not divide by zero. Canceling out the 2-2s is not allowed... because you can not divide by zero. Learn it, fear it, hate it and always be wary of it. Never let anyone else divide by zero... and when you hear someone say "let a = b = 1/2 so $a^2 = b^2 = ..." stop them right there and say "you're going to prove 1 = 0 by dividing by (b - a), aren't you?". Friends don't let friends divide by zero. – fleablood Jan 10 '16 at 00:41

3 Answers3

1

As @stef says, from the get go, when the denominator is zero, you have an indefinite value. Division operation in mathematics must yield a unique value. Division by zero violates this rule and that is why we can't process fractions containing zero in the denominator without care. Now, cancelling the value $(2-2)$ is not mathematically allowed since the value is zero in the denominator. Zeros are not allowed to be divided by. When working on mathematical problems, authors sometimes stress on this fact. For example, when you want to find the value of $y$ in $xy=6$, you divide both sides by $x$ to obtain $y=\frac{6}{x}$ however, this answer should be qualified by stressing on the range of x by specifying: "where x is not zero.".

Many references exist discussing this concept and anomalies that result-in from overlooking this, for example:Wikipedia-Division by zero, also Zero-divided-by-zero. Several other questions and answers about dividing by zero.

Community
  • 1
NoChance
  • 6,427
0

This is $\frac {0}{0}$, which isn't defined. Simplifying by $2 - 2 = 0$ doesn't make sense either. Note that in the equivalent $x \cdot 0 = 0$ x can take any value whatsoever.

vonbrand
  • 27,812
0

The expression $\frac{4-4}{4-4}$ has no well-defined value because it is just $\frac{0}{0}$.

I like the trick of factorising the numerator and denominator to give $\frac{(2-2)(2+2)}{2(2-2)}$.

However, when you try to cancel $(2-2)$ from both the numerator and denominator, you must ask yourself what it means to "cancel". When you "cancel the twos" to give $\frac{2}{6} = \frac{1}{3}$, what have you done? You have divided both the numerator and denominator by 2.

When you try to cancel the $(2-2)$ in your fraction, you are dividing both the numerator and denominator by $(2-2)$. The problem is $2-2=0$, and so you have divided both the numerator and denominator by zero. It's bad enough dividing by zero once, but you did it twice!

This kind of cancellation can work when you are dealing with limits. For example, what happens to $\frac{x^2}{x}$ as $x$ gets very small. It makes sense for all $ x \neq 0$. For example, when $x=3$, $\frac{x^2}{x}=\frac{9}{3}=3$. When $x=2$, $\frac{x^2}{x}=\frac{4}{2}=2$. When $x=1$, $\frac{x^2}{x}=\frac{1}{1}=1$. What about $x=0$? When $x=0$, $\frac{x^2}{x}$ is not well-defined and takes no value. However, we can first pretend that $x \neq 0$ and get $\frac{x^2}{x} \equiv x$. Then as $x \to 0$, we say that $$\lim_{x \to 0} \frac{x^2}{x} = \lim_{x \to 0} x = 0$$

Fly by Night
  • 32,272