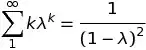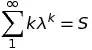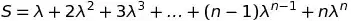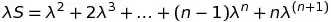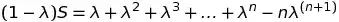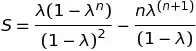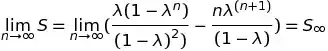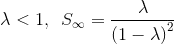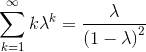I recently read a book about Data structures, int that book I found this equation under topic, "the average number of probes for an unsuccessful search":
but when I was trying to prove this I found another expression, here is how I tried:
So my proof led me to this equation
So what did I do wrong, I can't find any error above?
Or Am I right?
Your answer is right. $\lambda =0$ should give both the right hand side and left side to be zero, which is clearly not the case in the formula given in the text.
Another way to obtain the same answer is as follows. We have \begin{align} \sum_{k=0}^{\infty} \lambda^k = \dfrac1{1-\lambda} \,\,\, \forall \left \vert \lambda \right \vert < 1 \end{align} Differentiating the above we obtain \begin{align} \sum_{k=0}^{\infty} k\lambda^{k-1} = \dfrac1{(1-\lambda)^2} \,\,\, \forall \left \vert \lambda \right \vert < 1 \end{align} Multiplying by $\lambda$, we obtain \begin{align} \sum_{k=0}^{\infty} k\lambda^{k} = \dfrac{\lambda}{(1-\lambda)^2} \,\,\, \forall \left \vert \lambda \right \vert < 1 \end{align}
