Happened on this nice page, short version of one written by A. Baragar, https://www.encyclopediaofmath.org/index.php/Hurwitz_equation
You have a very slight variation of the originals; Hurwitz briefly considers adding a constant on the last page of his 1907 article. Indeed, the right hand side may be taken to be any sum of elementary symmetric polynomials, with integer coefficients. This includes, for example, Apollonian circle packing. In the Apollonian problem the solutions do not split up into trees, a phenomenon which is fairly easy to prove for this problem. Here is a good example of a problem with mixed symmetric functions that has the more typical behavior of finitely many trees. Diophantine quartic equation in four variables
This is related to the Markov Numbers. https://en.wikipedia.org/wiki/Markov_number
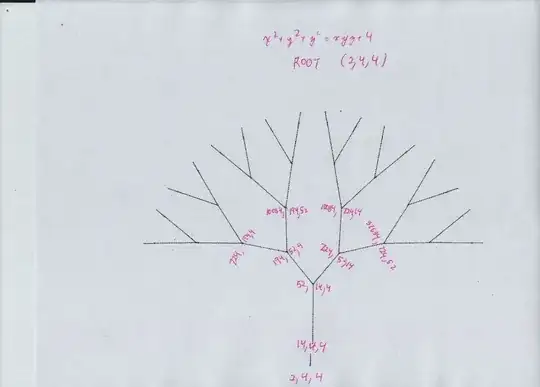
It is unusual that the solutions are gathered into an infinite number of trees, each with root solution $(2,t,t)$ as observed in another answer. This leads to a second "singular" solution $(t^2 - 2, t, t).$ After that we get triples with distinct elements. I did a small portion of the tree with root $(2,3,3).$

Travel within the tree is accomplished by three transformations: given a solution $(x,y,z)$ we get three other solutions
$$ (yz - x,y,z), $$
$$ (x, zx - y, z )$$
$$ (x,y,xy -z). $$
If anyone of these is done twice in a row, all that happens is a return to the beginning triple. For the vast majority of solutions, one of the transformations reduces $x+y+z,$ so that a careful choice of transformations eventually gets us to a root $(2,t,t).$ ALSO: any of the transformations make no change to $\gcd(x,y,z).$ Given that the root element is $(2,t,t),$ we get $\gcd(x,y,z)= 1$ when $t \geq 3$ is odd, but $\gcd(x,y,z)= 2$ when $t \geq 4$ is even.
The best reference for this sort of problem is Hurwitz (1907). A Hurwitz fundamental solution, in order, is $(x,y,z)$ with $x \geq y \geq z > 0,$ with the key condition being $2x \leq yz.$ we know that $(t,t,2)$ is a fundamental solution for $t \geq 2,$ and not an isolated solution when $t \geq 3.$ A little fiddling with indefinite binary quadratic forms shows that we do NOT have a fundamental solution if $z \geq 3.$ So, actual fundamental solutions are $(t,t,2).$ There is also an isolated solution $(2,1,1).$

Saturday, put this at the end. We have, for this problem, an infinite number of roots $(t,t,2).$ We could call these $x_1 \geq x_2 \geq x_3$ to better fit Hurwitz. He calls such a root a fundamental solution, or Grundlösung. His equation is
$$ x_1^2 + x_2^2 + \cdots x_n^2 = A x_1 x_2 \cdots x_n. $$
He takes
$$ x_1 \geq x_2 \geq x_3 \geq \cdots \geq x_n. $$
A Grundlösung also satisfies
$$ 2 x_1^2 \leq A x_1 x_2 \cdots x_n. $$ On page 189, he reaches formula (15) for fundamental solutions,
$$ A x_3 x_4 \cdots x_n \leq n. $$
Thus there are finitely many such $A$ and $x_3 \geq \cdots \geq x_n. $
Finally, when $x_1 = x_2,$ we get
$$ 2x_1^2 + x_3^2 + \cdots x_n^2 = A x_1^2 x_3 \cdots x_n, $$ or
$$ ( A x_3 x_4 \cdots x_n - 2) x_1^2 = x_3^2 + x_4^2 + \cdots x_n^2 $$
For each of the finitely many such $A$ and $x_3 \geq \cdots \geq x_n, $ there is at most one $x_1.$ All together, there is finiteness when $x_1 = x_2$ in the Hurwitz-Markov equation. Indeed, when $n=10,$ there are three,
$$ A = 10, (1,1,1,1,1,1,1,1,1,1), $$
$$ A = 4, (2,2,1,1,1,1,1,1,1,1), $$
$$ A = 1, (4,4,3,1,1,1,1,1,1,1). $$
Largely because of the constant term $4,$ the problem in this question has infinitely many fundamental solutions $(x_1, x_1, 2),$ where we have been calling $x_1 = t.$


