Quadratic equations amount

Question

Quadratic equation looks like that: $$ax^2+bx+c=0$$ where $a\ne 0$. We can say something about roots when We compute a discriminant $$\Delta=b^2-4ac$$ When $\Delta>0$ then We have two real roots, when $\Delta<0$, then two imaginary roots. Can We say enything about amount of thise equations in finite set of coefficients? E.g. when $a,b,c\in\{1,2,...,n\}$ then We have $n^3$ different equations. I prepared graphs when $a,b,c\in\{1,2,...,i\}$ and $i$ is on horizontal axis. On vertical axis there is amount of particular equations.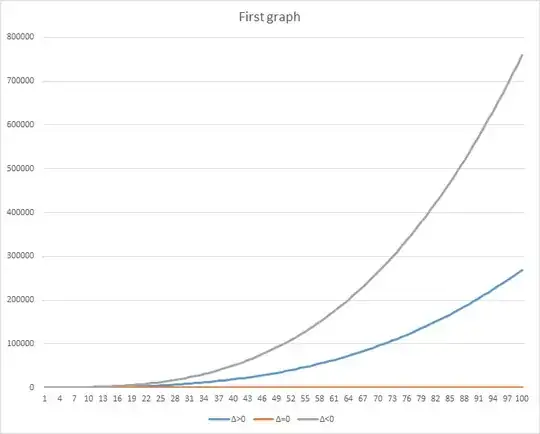

At the first I thought that this is because of asymmetric shape of formula for $\Delta$. $ac$ is multipled by $4$. When I divide amount of $\Delta<0$ equantions by $4$, then I got:

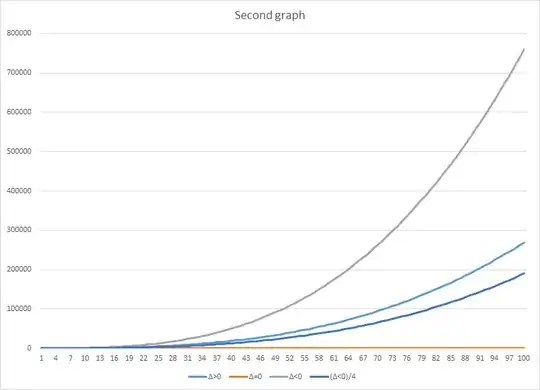
Is there any theorem or results about that? Maybe in countinuous sets We can say something about ratios?

Answer 1

If $N$ is the number of equations with $\Delta < 0$, the number of equations with $\Delta > 0$ seems to be much closer to $N/3$ than to $N/4$. That is, for every $4$ equations, on average, we typically get one equation where $\Delta > 0$ and the other three have $\Delta < 0$. You could work out the asymptotic behavior of this ratio by considering the probability that $X^2 > 4YZ$ where $X$, $Y$, and $Z$ are iid uniform continuous random variables.

So yes, we can say something about ratios, and very likely someone already has do so.