4

Let $a, b \in \mathbb{R}^2$ be two points in the plane and let $\Pi$ be their perpendicular bisector (see left figure). Let $c \in \Pi$ be any point and consider the triangle $\triangle abc$. Suppose that there is another point $p \in \operatorname{Int}{\triangle abc}$. It's easy to see that $d(c, p) < d(c, a) = d(c, b)$. Is the same true of a geodesic triangle on a surface $\Sigma \subset \mathbb{R}^3$? In this case we consider the intrinsic metric $d_{\Sigma}$ defined by shortest paths on the surface $\Sigma$. We then define the 'perpendicular bisector' as the set of all points equidistant to $a, b \in \Sigma$ with respect to the metric $d_{\Sigma}$. (See right figure.)

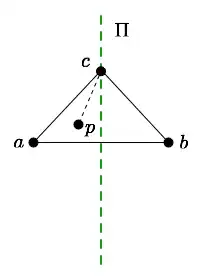
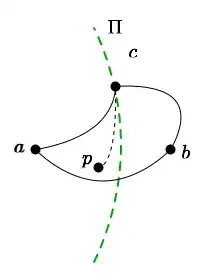
enter image description here enter image description here

Edit: I don't think this is true since the height of the surface could increase rapidly within the interior of the triangle. A side view, looking down in the direction of $\vec{ab}$, of what I'm talking about might looking like the following figure.

enter image description here

In which case, can I prove the result if I assume a bound on the principal curvatures in the interior of the triangle?

user296029
  • 55
  • So $\Sigma$ is your (deep) coffee mug and $\Pi$ is the symmetry line of your coffee mug. Let's say $a$ and $b$ are on the rim (where your mouth makes contact to take a sip, $b$ if you're right handed, $a$ if left handed). Now if $c$ is on the rim, too and $p$ is down at the bottom of the mug, it could be shorter to get from $a$ to $c$ by walking along the rim than to dive down from $c$ to $p$. This depends on how deep the coffee mug is compared to the perimeter of its rim. I'm not sure I understand your question so I leave this as a comment. – null Jan 05 '16 at 22:42
  • @null It seems you responded as I was editing! Yes, that example is the same reasoning as my edit. – user296029 Jan 05 '16 at 22:46

2 Answers2

1

To confirm it's not true with a concrete example:

Take three points on the equator of the unit sphere, equispaced, as your triangle. Then the distances are each $2\pi/3 \approx 2.1$. But the distance from one point, up over the north pole, to the far side, is $\pi$, which is considerably larger.

I also think that there's no theorem to be had here.

Consider two concentric equilateral triangles in the plane. Lift the inner one up along the plane normal. And now blend from the inner triangle to the outer one smooothly. (It's perhaps easier to see this with concentric circles. Fill in the raised inner circle with a flat disk, and around the edge of the raised inner circle, add a 1/4-circle at each point, joining smoothly to the disk, and turning downward.)

Do the same think to the larger, lower circle, but with the "flange" interior to the circle, and rising up.

Now join these two flanges with a cylinder. The cylinder can be arbitrarily long. If you place three vertices equidistant along the bottom circle, they form a triangle for which interior segments can be very long.

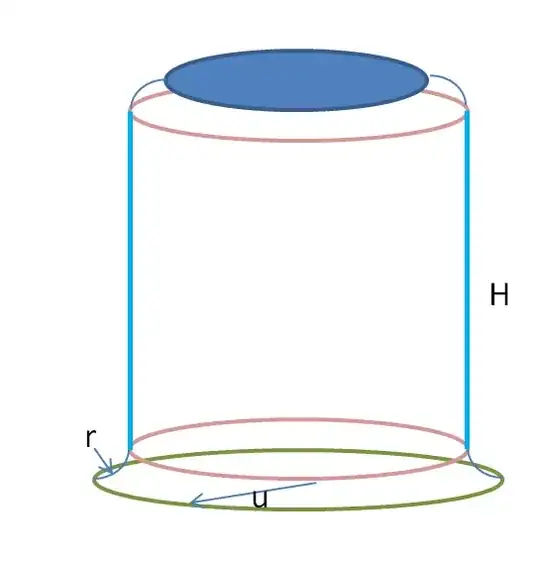
Here's a (rough) picture: enter image description here

The "inner circle" bounds the blue disk at the top. The small blue quarter circle is revolved about the vertical axis to form a little "flange" that joins this top disk to the vertical bright-blue cylinder. A similar "flange" joins the bottom of the vertical cylinder to the large (green) circle at the bottom.

By making the bottom radius $u$ large, and making $r = \frac{u}{4}$, say, the principal curvature of the flanges in the radial direction is $\frac{1}{r} = \frac{4}{u}$, which is small, and in the azimuthal direction, it's no more than the curvature of the red circles, which have radius at least $u/2$, hence curvature at most $\frac{2}{u}$. So for large $u$, I can make the principal curvatures arbitrarily small (and the Gaussian curvature as well, of course). But the arc that starts at the bottom left corner of the pic, follows the blue line labelled "$r$", then the bright blue line, then the next quarter-circle, straight across the blue disk, and down the other side...that has length $2 \pi r + 2H = \frac{\pi u}{2} + 2H$. Since $H$ is arbitrary, I can, with a curvature-bounded surface, get an interior ray of a triangle (the "triangle" being three points on the bottom green circle) whose length is an arbitrary multiple of the edge lengths.

John Hughes
  • 93,729
  • How does one bound the gaussian curvature using Gauss-Bonnet? The statement of that theorem is an equality. – user296029 Jan 06 '16 at 01:02
  • I've re-thought it, and rewritten the answer. I don't believe that there's a theorem lurking here, at least not easily. – John Hughes Jan 06 '16 at 01:24
  • I don't think I fully understand your example, in particular the last part with the cylinder, but I really think there should be some true statement here if a bound on curvature is assumed. If I assume an upper bound on the curvature, in the limiting case, as the curvature approaches zero, the geodesic triangle approximates a Euclidean triangle, for which the statement is true. It seems that an $\epsilon$ perturbation shouldn't change that. – user296029 Jan 06 '16 at 01:39
  • See illustration and added explanation. – John Hughes Jan 06 '16 at 02:22
1

(a) In general this is not true : Define $\Sigma = ( \mathbb{R}^2-B_\epsilon (O) ) \cup_{\partial B_\epsilon (O) } S \subset \mathbb{R}^3$ where $S=B_\epsilon(O)$ has a metric $g$ s.t.

(1) It is rotationally symmetric

(2) It has positive curvature

(3) $d_g(O,\partial B_\epsilon (O))$ is suitably large

Here we can give smooth structure on $\Sigma$ by perturbation without a lot of loss of the above property

(b) Assume that $(\Sigma,g)$ has nonpositive Gaussian curvature

Then consider a geodesic triangle $\triangle cab$ in $\Sigma$ Then we have corresponding triangle $\triangle CAB$ in $\mathbb{R}^2$ s.t. side lengths are equal

Then if $p$ is in geodesic from $a$ to $b$, then $$ d_g(c,p)\leq |CP| \leq |CA|=d_g(c,a) $$ where $|\ |$ is a canonical metric on $\mathbb{R}^2$ and $ d_g(a,p)=|AP|$

HK Lee
  • 19,964