The problem:
There are n different kinds of coupons, and we need to get every kind of coupon at least once to win. Each time we get new coupons we get them in a batch of k coupons where k ≤ n (the same coupon can appear multiple times in the batch of k coupons).
Let Xk,n be a random variable that denotes the number of batches we need to buy to collect all the n different coupons.
I already know and understand how to calculate the expected value when k=1 (that is the classic coupon collector problem), but have difficulty calculating E[Xk,n] for k > 1.
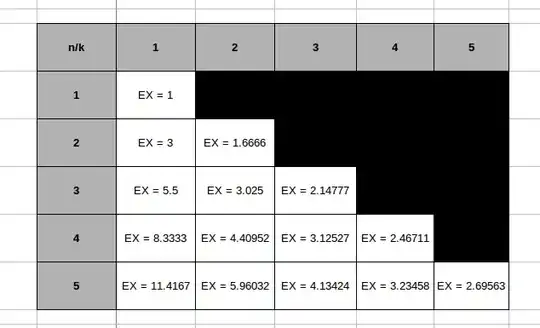
If it helps, I've also made some simulations and estimations, and came up with this table: