5

Consider the following situation.

You are standing in a room that is perfectly circular with mirrors for walls. You shine a light, a single ray of light, in a random direction. Will the light ever return to its original position (the single point where the light originated from)? If so, will it return to its position an infinite amount of times or a definite amount of times? Will it ever return to its original position in the original direction?

I thought of this little teaser when reading about a problem concerning rays in a circle and wondered about this question.

As for my attempts, this is well beyond my skill.

Simply Beautiful Art
  • 74,685
  • Is the "original position" a point or a region (for the flashlight and/or your body)? Are you asking for the probabilities involved? – Rory Daulton Jan 05 '16 at 01:03
  • @RoryDaulton It is a point. I will make sure that is easy to understand. – Simply Beautiful Art Jan 05 '16 at 01:13
  • 1
    If you are on the circonference then the ray will return if and only if you shoot at an angle (respect to the tangent) which is a rational multilple of $\pi$, and it will return in a finite amount of time. If you are not in the circumference then again if you shoot at rational multiple of $\pi$(respect to the tangent of the hitting point), it will return. Not sure what happens in this case if you shoot with a different kind of angle. – mrprottolo Jan 05 '16 at 01:37

4 Answers4

4

This can be solved completely by characterizing the set of points on the ray which are the same distance from the center as the original point. We consider two symmetries which generate all such points. Here is a diagram showing all the points we consider:

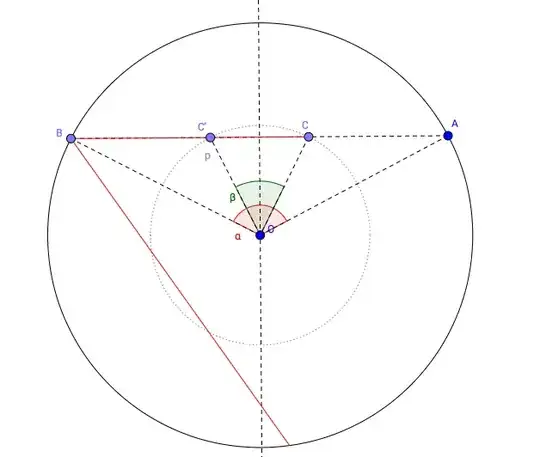
enter image description here

In particular, if our initial point is $C$, consider the line $AB$ which is coincident with the ray and which has $A$ and $B$ both on the unit circle and $B$ in the forwards direction of the ray. This segment would be visible if you shot a ray in either direction, and it did not bounce. Notice that, if $O$ is the center of the circle, then the angle $\alpha=\angle AOB$ is significant since rotating by $\alpha$ (in the same direction as the rotation that takes $B$ to $A$) takes one segment of the ray to the next segment after it bounces.

One may notice that this rotation preserves the distance from the center of the circle - so every point ever at this distance in any segment of the light's path is such a rotation of one at that distance on $AB$. There may be at most two such points - the point $C$ itself, and the point $C'$ which is the reflection of $C$ through the perpendicular bisector of $AB$. Let us set $\beta=\angle COC'$ which should be taken as a signed angle - so if the rotation taking $C$ to $C'$ is the opposite direction as the one taking $A$ to $B$, we take $\beta$ to be negative. We will always consider $\alpha$ to be positive.

Notice that if the ray returns, then there is some non-trivial rotation taking $C$ to itself. That means that one of the following is true (for some integers $n,k$): $$n\alpha = 2\pi k$$ $$n\alpha + \beta = 2\pi k.$$ This completely characterizes the problem. One should note that any point inside a circle along with a ray extending from it may be described up to rotation and reflection by a pair $(\alpha,\beta)$ with $0\leq \alpha \leq \pi$ and $|\beta|\leq \alpha$.

The case of $C$ being on the circumference corresponds to the case $|\beta|=\alpha$. One should note that the first set of solutions is just when $\alpha$ is a rational multiple of $\pi$, in which case the ray is truly periodic. Moreover, if $\beta$ is a rational multiple of $\pi$, then the second set of solutions doesn't add any new solutions for $\alpha$ (meaning that if the ray ever returned, it would be bouncing periodically).

Milo Brandt
  • 60,888
  • Nice approach. Since chosen $C$ and $\alpha$ is not obvious what will be $\beta$, do you think it is possible that for some $C$ there exist only one angle $\alpha\neq k\pi$ for which the ray will return? – mrprottolo Jan 05 '16 at 10:03
  • @mrprottolo I'm not sure. A related statement is that, except for at the center or on the circumference, there exist infinitely many solutions of the form $n\alpha + \beta = 2\pi k$. However, we could still get unlucky if all the $\beta$ happen to be rational multiples of $\pi$ (which is more or less what happens on the circumference). It's worthy of note that to fix a point $C$, we just fix the quantity $\frac{\cos(\alpha/2)}{\cos(\beta/2)}$ which is the distance of $C$ from the center. – Milo Brandt Jan 05 '16 at 16:56
  • So the problem reduces to: given$0<d\le1$, to find $\alpha$ such that $$n\alpha +2\arccos(\frac{\cos (\alpha /2)}{d})=2k\pi$$ for some $n,k \in \Bbb Z$. This looks hard. – mrprottolo Jan 05 '16 at 17:03
  • @mrprottolo You want $n\alpha + 2\arccos(d\cos(\alpha/2))=2k\pi$. You could also simplifying (by taking $\alpha$ and $\beta$ to be the half-angles) to finding solutions to $n\alpha + \arccos(d\cos(\alpha)) = k\pi$. I agree that that looks hard. – Milo Brandt Jan 05 '16 at 17:10
2

Not a complete answer.

Case -1- You are in the circumference. The ray will return if and only if the shooting angle is $k\pi$ with $k\ \in \Bbb Q$.

Case -2- You are not in the circumference and you shoot at angle of $k\pi$. If you draw the line passing through the start position and the first hitting point it interects the circumference in a third point $A$. Now if you shoot from $A$ at the same angle, you are in case -1-, and you will return to $A$ and as a consequence you will return to the starting position immediately after.

Case -3- You are not in the circumference and you shoot at angle $\theta$ that is an irrational multiple of $\pi$. In this case it is possible to return, here is why. Take a point $A$ in the circumference and a shoot a ray with angle $\theta$ and call $B$ the first hitting point. Now if you follow the path of the ray, you will for sure interects the segment $AB$ in a point $C$. Hence if you start from $C$ and shoot a ray to $B$(with angle $\theta$) you will return to $C$.

Comments: It remain possible the case where you shoot from a point inside of the circle, but never return. Notice also that in the last case the ray will intersect the segment $AB$ infinitely many times in always a different point, so there are infinite choices for $C$.

mrprottolo
  • 3,792
1

Once the ray of light hits the wall for the first time, it will bounce off at a certain angle. Since all points on a circle are essentially the same, the question is: if a ray departs from a point $A$ on a circle at an angle $\theta$ (from the radius at that point), where will it go?

Look at the following diagram.

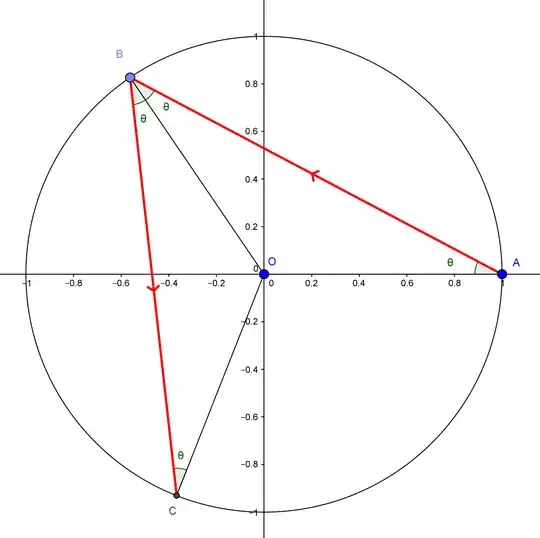
enter image description here

The equality of the angles $OAB$ and $OBA$ is justified since $AOB$ is an isosceles triangle. The equality of $ABO$ and $OBC$ is justified by the law of reflection, combined with the fact that the radius $OB$ is normal to the circle at $B$. These arguments can be continued to show that every time the ray hits the mirror, it will do so at an angle of incidence $\theta$!

Now, the points $A$, $B$, $C$ at which the light hits the mirror are the first in a sequence $A = x_0, x_1, ...$ of points. What are the polar coordinates of these points? The angular coordinate of $A = x_0$ is of course $0$. And $B=x_1$? Looking at the diagram, we can see it's $\pi - 2\theta$. In fact, it should be clear that the angular coordinate of $x_n$ is $n(\pi - 2\theta)$.

Thus, we can forget about the ray of light and laws of refraction. We are simply interested in a sequence of angles $n\alpha$ for some angle $\alpha$. Is it periodic, for instance? Since $n\alpha$ is the argument of $(e^{i\alpha})^n$, we can also view this as a question about complex numbers, a question which is well known and solved. In short, the answer is: if $\alpha/\pi$ is rational, the sequence is finite (and thus periodic). Otherwise, the sequence is dense in the circle, that is, your ray of light eventually hits more or less every point in the circle.

The questions about which points inside the circle the light crosses as it does this (does it return to its original position, etc) can probably be deduced from the above facts. Certainly the light will never return to its original position with the same velocity vector unless $\alpha/\pi$ is rational (in which case it will), since this is equivalent to the sequence $n\alpha$ being periodic.

If $\alpha/\pi$ is not rational, the set of points on the circle struck by the ray is dense in the circle, thus I imagine the set of points the light passes through is probably dense in the disk, though I suppose it might not be. If so, we can at least say the light will pass arbitrarily close to its starting point.

Community
  • 1
Jack M
  • 27,819
  • 7
  • 63
  • 129
  • 2
    It is possible for the ray to return also in the case that the angle is irrational and you are inside the circle, see my answer. – mrprottolo Jan 05 '16 at 01:59
  • 1
    @mrprottolo If I didn't make any mistake, if $\alpha/\pi$ is irrational, the ray can return to the starting spot but at most once. – achille hui Jan 05 '16 at 02:40
  • I wonder, taken $A$ inside the circle, which are the irrational angles for which the ray will return to $A$. – mrprottolo Jan 05 '16 at 02:54
0

It is more of optics/physics. If the room is cylindrical, the ray goes out to infinity.

If it is spherical then wlog consider originating ray to be at minimum distance from center $r<R$ where $R$ is sphere radius.

As the incident and reflected rays are equal by laws of reflection all rays are confined in a plane containing initial ray and the sphere center.

When $$ n= \dfrac{\pi}{\cos^{-1} \frac{r}{R}} $$

is an integer then the rays retrace their own path on boundary of a regular polygon of $2 n$ sides, else all rays are confined in the ring of extreme radii $r,R.$

Ditto for cylindrical mirror tube when starting ray , the axis of cylinder and radius are mutually orthogonal.

Narasimham
  • 40,495