Regarding why the $dy$ and $dx$ show up, the short answer is "because of the chain rule." In these situations, we're trying to solve for $y$ in terms of $x$, right? That means we're assuming at the outset that $y$ is a function of $x$! You know that $k$ is a constant, here, so $$\frac{d}{dx}\left[k^2\right]=0,$$ which you calculated just fine. Now what if the other side looked like $x^2+2(f(x))^2$? Well, then by the chain rule, we have $$\frac{d}{dx}\left[x^2+2(f(x))^2\right]=2x+2\cdot\frac{d}{dx}\left[(f(x))^2\right]=2x+4f(x)f'(x),$$ or, written another way, $$\frac{d}{dx}\left[x^2+2(f(x))^2\right]=2x+4f(x)\frac{df}{dx}.$$ Since in this particular situation, we are assuming $y=y(x)$ is a function of $x$, then applying $\frac{d}{dx}$ to both sides gives us $$2x+4y\frac{dy}{dx}=0,$$ That's why the $\frac{dy}{dx}$ is there.
The only potential problem, here, is that $\frac{dy}{dx}$ may be undefined in some places, so let's look at another way we can deal with that.
If instead we simply apply the differential operator $d$ to both sides, the right side would still become $0$, as a derivative of a constant. On the other side, we would have $$d\left[x^2+2y^2\right]=d\left[x^2\right]+2\cdot d\left[y^2\right]=2x\,dx+4y\,dy,$$ so $$2x\,dx+4y\,dy=0.$$ For some more details, refer back to the discussion of the differential operator in my answer to this question.
Now, if given a general equation $Au+Bv=0$--with $2$-dimensional coordinates $(u,v)$--for a line passing through the origin, what would be the equation of the perpendicular line passing through the origin? We can't necessarily use a slope-type argument (the line could be vertical, after all), but it is a good exercise to prove that $-Bu+Av=0$ is a general equation for the corresponding perpendicular line, regardless of the constants $A,B$.
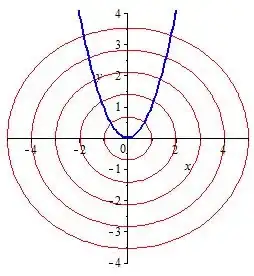
Here, we have a similar situation, with $u=dx$, $v=dy$--tangent lines can be vertical, after all, as you should be able to see from the level curves in the picture from Babak's answer--so instead of talking about $\frac{dy}{dx}$ as the slope of the tangent line at the point $(x,y)$, we can instead stick with the general form $$2x\,dx+4y\,dy=0\tag{#}$$ of the parallel line through the origin. There are three cases that we must consider, here: (1) $x,y\neq 0$, (2) $x\neq 0$ and $y=0$, (3) $x=0$ and $y\neq 0$. Why needn't we consider the case that $x,y=0$? Because in that case, we are considering the equation with $k=0$, which has only $(0,0)$ as a solution--that is, it isn't a curve, but a point, so we can't really talk about tangent lines in any meaningful sense.
Case (1): Suppose that $x,y\neq 0$. The perpendicular line to $(\#)$ through the origin will then have form $-4y\,dx+2x\,dy=0$, or equivalently $$\frac{1}{2y}\,dy=\frac{1}{x}\,dx,$$ which describes the orthogonal trajectory (OT) curve to $x^2+2y^2=k^2$ at the point $(x,y)$. Integrating yields (as in Babak's answer) $$\frac{1}{2}\ln|y|=\ln|x|+c.$$ Since you've got both $y$ and $x$ "trapped" in natural logarithms, you really want to get them out, and the best (really only) way to do that is through exponentiation. You're trying to solve for $y$, so let's begin by isolating $\ln|y|$, yielding $$\ln|y|=2\ln|x|+2c=\ln(|x|^2)+2c=\ln(x^2)+2c$$ through log rules. Now exponentiating both sides of the equation base $e$, we have $$|y|=e^{\ln(x^2)+2c}=e^{\ln(x^2)}e^{2c}=Cx^2,$$ where $C=e^{2c}$. We're still not quite there, yet, since $y$ is still in absolute value, but it will either be $y=Cx^2$ or $y=-Cx^2$. Thus, the OT curve passing through $(x,y)$ in this case will be of the form either (a) $y=Kx^2$ ($x>0$) or (b) $y=Kx^2$ ($x<0$)--where $K$ (you should see) is in either instance some non-$0$ real constant determined by $x$ and $y$.
Case (2): Suppose $x\neq 0$ and $y=0$, then $(\#)$ becomes $2x\,dx+0\,dy=0$, and the perpendicular is $0\,dx+2x\,dy=0$, or equivalently (rearranging and dividing by $2x$), $dy=0\,dx$. Integration yields $y=c$, and given what we know about $y$, we have $c=0$. Thus, in this case, the OT curve passing through $(x,y)$ is either (a) $y=0$ ($x>0$) or (b) $y=0$ ($x<0$). Note that we can still write this in the form $y=Kx^2$--it is just that $K=0$ in this case.
Hence, we can combine cases (1) and (2), so that if $x\neq 0$, then the OT curve passing through $(x,y)$ has the form either (a) $y=Kx^2$ ($x>0$) or (b) $y=Kx^2$ ($x<0$)--where $K$ is some real constant determined by $x$ and $y$.
Case (3): Similarly to case (2), we find that the OT curve has form either (a) $x=0$ ($y>0$) or (b) $x=0$ ($y<0$). How can we talk about such a curve in terms of curves $y=Kx^2$ ($x>0$) or $y=Kx^2$ ($x<0$)? Well, the one from (a) can be obtained as a limit of such curves as $K\to+\infty$, and the one from (b) can be obtained as a limit of such curves as $K\to-\infty$.
Remark: In cases (2) and (3), it should be clear that the $4$ open rays described are the relevant OT curves, if one simply looks at the level curves associated to each $k$. Still, we may find them explicitly as above.