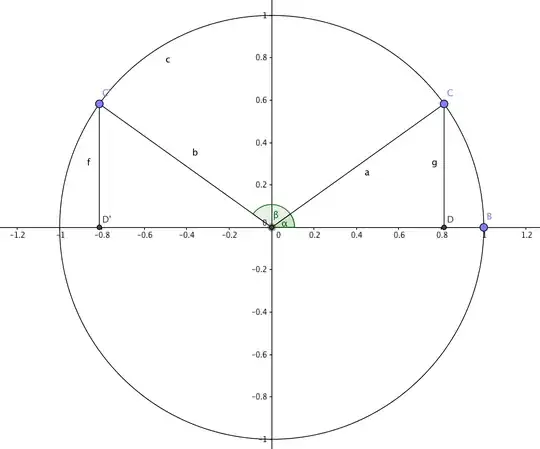
I have been trying to think of a clear and concise way of explaining why if angles $a$ and $b$ add up to $180$ degrees, $\cos(a) = -\cos(b)$. I came up with a way where I sketch $a$ and $b$ on the $x$ axis of the cosine curve, and observe the inversion symmetry about $90$ degrees. However there must be a more obvious and complete way.
Asked
Active
Viewed 1,371 times
1
-
Hint: Write $b = 180 - a$ – Simon S Jan 01 '16 at 20:56
-
1Do you know things like $\cos(x)=\cos(-x)$ or $\cos(x+180^{\circ})=-\cos(x)$? – Milo Brandt Jan 01 '16 at 20:56
-
Draw a graph with a ray from the origin at angle $ \ a \ $ counter-clockwise from the positive $ \ x-$ axis; $ \ b \ $ is the supplementary angle. Now "flip" the graph about the $ \ y-$ axis: what do you observe about the cosines of the two angles? – colormegone Jan 01 '16 at 20:59
-
Related (enough to be a duplicate?): "How to remember a particular class of trig identities." – Blue Jan 01 '16 at 21:05
4 Answers
6
$\cos(b)=\cos(180-a)=\sin(90-180+a)=\sin(a-90)=-\sin(90-a)=-\cos(a)$
1
Hint: $\cos(x-y)=\cos(x)\cos(y)+\sin(x)\sin(y)$
Use $a=\overbrace{180^\circ}^x-\overbrace{b}^y$.
robjohn
- 345,667
-
Would the downvoter care to comment? (He asked, expecting the answer, "no".) – robjohn Jan 05 '16 at 08:32
1
If angles $a+b = 180$ then $ a = 180-b$. Now, using the identity $\cos(x+180) = -\cos(x)$ and substituting with $a$ and $b$ we have $\cos(a +180) = -\cos(a) $ and remembering that $a=180-b$, then $\cos(180-b+180) = -\cos(a)$ so $\cos(b) = -cos(a)$ when angles $a+b =180$.
j.d. allen
- 759