$$ \lim_{x\to 0+} \sin\left(\frac{1}{x}\right)$$ I know that there is no limit.
but, why there is no limit? I tried $x=0.4$, $x=0.3$, $x=0.1$, it looks like the limit is $0$.
And how can I show that there is no limit? I tried to calculate it like all the other functions, and I got wrong result and I don't know why:
$$\lim_{x \to 0+} \sin\left(\frac{1}{x}\right) = \sin\left(\frac{1}{0^+}\right) = \sin\left(\frac{1}{\infty}\right) = \sin(0) = 0.$$
Why there is no limit?
The graphic can help you understand why and suggest you some approach for the proof:
Remark: You have to be careful with tables of values because they can be misleading:
\begin{array}{ c | c c c c } x & \frac{1}{2\pi} & \frac{1}{3\pi} & \frac{1}{4\pi} &\frac{1}{5\pi} \\ \hline \sin\left(\frac{1}{x}\right) & 0 & 0 & 0 & 0 \\ \end{array}
\begin{array}{ c | c c c c } x & \frac{2}{5\pi} & \frac{2}{9\pi} & \frac{2}{13\pi} &\frac{2}{17\pi} \\ \hline \sin\left(\frac{1}{x}\right) & 1 & 1 & 1 & 1 \\ \end{array}
(The tables above are a sketch of the proof - see Theorem 2.4 here.)
That's because your limit is equivalent to $$\lim_{x\to\infty} \sin(x)$$
and $\sin$ is oscillating when $x\to\infty$.
Hint: $\frac1x$ has a right-sided limit of $+\infty$. Does $\sin x$ have a limit for $x\to\infty$?
You made an error. \begin{array}{ c | c c c c } x & .4 & .3 & .2 &.1 \\ \hline \sin\left(\frac{1}{x}\right) & 0.5984721 & -0.190568 & -0.9589243 & -0.54402113 \\ \end{array} This does not suggest that the limit approaches $0$.
Second, you mean to say $$\lim_{x\to 0^+} = \sin\left(\frac{1}{x}\right) = \sin(\infty)$$ not $\lim_{x\to 0^+}\sin\left(\frac{1}{x}\right) = \sin\left(\frac{1}{\infty}\right).$ Recall that $$\lim_{x\to 0^+} \frac{1}{x} = \infty.$$
Consider the two subsequences $x_k = \frac1{(4k + 1)\pi/2}$ and $x'_k = \frac1{k\pi}$ with $k \in \mathbb Z$. We have that for $k \to +\infty$, $x_k,x'_k \to 0^+$. Clearly, $$\begin{align*} &\lim_{k \to +\infty} \sin\left(\frac1{x_k}\right) = 1\\ &\lim_{k \to +\infty} \sin\left(\frac1{x'_k}\right) = 0 \end{align*}$$ and therefore the limit $x \to 0^+$ does not exist. We used the theorem that states that if a sequence converges, then every subsequence converges to the same limit. By modus tollens, our sequence does not converge.
More info about the theorem here: Prove: If a sequence converges, then every subsequence converges to the same limit.
Lets look at $sin(\frac{1}{x}) $ function,
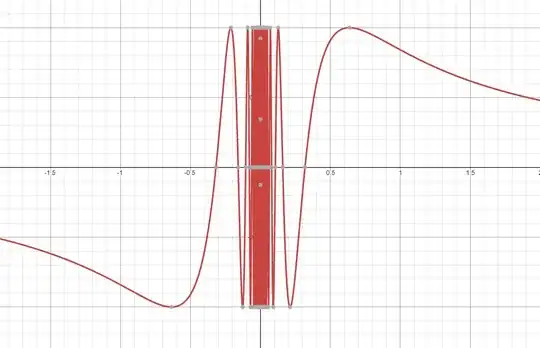
Now you can get a idea how it behaves near to 0. That is oscillating near 0. THat's why we can't get limit when x goes to 0 of $sin(\frac{1}{x}) $ function. So let's move into it's proof,
$$\forall \varepsilon >0 \; \exists \delta \; s.t \; 0< x < \delta \mapsto |sin\frac{1}{x}-L|<\varepsilon$$
Let $\varepsilon=\frac{1}{2}$,
$$0< x < \delta \mapsto |sin\frac{1}{x}-L|<\frac{1}{2}$$
Assume that, $$\lim_{x \to 0+} sin(\frac{1}{x})=L \; \in \mathbb{R}$$
Let $$x_{1}=\frac{1}{2n\pi+\frac{\pi}{2}} \; \; (n\in Z^{+})\; \; and \; \; x_{2}=\frac{1}{2n\pi+\frac{3\pi}{2} } \; \; (n\in Z^{+})$$ So we have to get range of n, $$0<\frac{1}{2n\pi +\frac{3\pi}{2}} < \frac{1}{2n\pi+\frac{\pi}{2} }<\delta$$ $$\frac{1}{2n\pi+\frac{\pi}{2} }<\delta$$ So we get, $$\frac{1}{2\pi\delta }-\frac{1}{4}<n\; \; (n\in Z^{+})$$
Now, $$|sin(x_{1})-L|=|1-L|<\frac{1}{2}\Rightarrow \mathbf{C}$$ $$|sin(x_{2})-L|=|-1-L|=|1+L|<\frac{1}{2}\Rightarrow \mathbf{D}$$ By C + D we get, $$|1-L|+|1+L|< 1$$ $$|(1-L)+(1+L)|\leq |1-L|+|1+L|< 1$$ $$2\leq |1-L|+|1+L|< 1$$ $$2<1 \; \;\; \; (\therefore contradiction)$$
Assumption is not true. $\: \: \therefore\:\lim_{x \to 0+} sin(\frac{1}{x})$ has no limit.
