Calculate $\int_0^{1}\frac{x^{-1 - x}\,\,\,\left(1 - x\right)^{x - 2}}{\mathrm{B}(1 - x\,, \,x)}\,\mathrm{d}x$

Question

How does one calculate $\displaystyle{\int_0^{1}\frac{x^{-1 - x}\,\,\,\left(1 - x\right)^{x - 2}} {\mathrm{B}(1 - x\,,\,x)}\,\mathrm{d}x}$ ?.

The observation $\displaystyle{\int_0^{1}\frac{x^{-1 - x}\,\,\,\left(1 - x\right)^{x - 2}}{\Gamma\left(1 - x\right)\Gamma\left(x\right)}\,\mathrm{d}x = \int_0^{1}\frac{x^{-1 - x}\,\,\,\left(1 - x\right)^{x - 2}} {\mathrm{B}(1 - x\,,\,x)}\,\mathrm{d}x}$ seems useless here.

The answer, according to wolfram, is $2$.

Answer 1

The conjecture of exact equality to $\:2\:$ is based on numerical calculus from WolframAlpha. The result of integration depends on the accuracy of the numerical calculus and also how the end of the calculus is specified. In a first approximate, the returned value is rounded to $\:2.\:$ (without specification of accuracy).

If we change a little bit the formulation in order to make WolframAlpha perform more accurate calculus, the result is non longer exactly $\:2\:$ but :
$$I=\displaystyle \int_0^{1}\frac{x^{-1-x}(1-x)^{x-2}}{\mathrm{B}(1-x, ~x)}\,{dx}=\displaystyle \frac{1}{\pi}\int_0^{1}x^{-1-x}(1-x)^{x-2}\sin(\pi x)\,{dx}$$ $$I\simeq 2.0000000204004$$ http://www.wolframalpha.com/input/?i=NIntegrate%5Bx%5E%28-1-x%29%281-x%29%5E%28x-2%29sin%28pix%29%2Fpi%2C%7Bx%2C0%2C1%7D%5D-2

So, the conjecture is numerically verified with an accurracy of about $\:2.10^{-8}\:$. This is far to be enough. Many coïncidences of that kind can be found without exact equality. In the technics of numerical identification, a relative accuracy of at least $\:10^{-18}\:$ is recommended at least. A paper on this subject : https://fr.scribd.com/doc/14161596/Mathematiques-experimentales (in French, not translated yet).

Regarding the resultat from WolframAlpha, with a discrepancy of about $\:2.10^{-8\:}$ the conclusion should be : the conjecture is false. But one have to be cautious because the accuracy of the numerical integration is not assured : So, the numerical test is inconclusive.

On the other hand, with another software the result was : $$I\simeq 1.999999999999938$$ which supports the view that the conjecture might be true.

Answer 2

I will write an outline of the proof that the integral in OP is $2$. If some intensive calculation is needed, I will put (*k) with increasing numbers k, but not include the calculation.

The same method as in this is applied. We define the function $f(z)$ same as above. To recall, it is $$ f(z)=\exp(i\pi z + z \log z + (1-z)\log(1-z)),$$ where $-\pi\leq \arg z < \pi$ and $0\leq \arg(1-z) < 2\pi$. But, in this problem, we need $g(z)$ where $$ g(z) = f(z)^{-1}. $$ We now consider the integral of $g(z)/(z(1-z))$ along the following contour:

1. Fix a small $\delta>0$ and a small $\epsilon>0$.

2. Draw two circles with radius $\epsilon$ centered at $0$ and $1$ respectively. We will call the circle centered at $0$ as $L_{\epsilon}$, centered at $1$ as $R_{\epsilon}$.

3. Erase a part of $L_{\epsilon}$ consisting of a smaller arc between $\epsilon e^{-i\delta}$ and $\epsilon e^{i\delta}$, and erase a part of $R_{\epsilon}$ consisting of a smaller arc between $1-\epsilon e^{i\delta}$ and $1-\epsilon e^{-i\delta}$. We will call the remaining arcs $L_{\delta, \epsilon}$ and $R_{\delta, \epsilon}$ respectively.

4. Connect the points $\epsilon e^{i\delta}$ and $1-\epsilon e^{-i\delta}$ by a straight line segment $U_{\delta,\epsilon}$, and connect the points $\epsilon e^{-i\delta}$ and $1-\epsilon e^{i\delta}$ by a straight line segment $D_{\delta,\epsilon}$.

5. We call this closed contour as $\Omega_{\delta,\epsilon}$.

The contour looks like this: 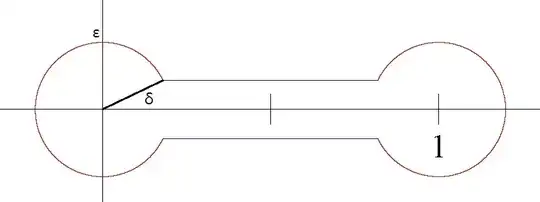Then by Cauchy residue theorem, we have $$ \int_{\Omega_{\delta,\epsilon}} \frac{g(z)}{z(1-z)} dz = -\mathrm{Res}_{z=\infty} \frac{g(z)}{z(1-z)} = 0. \ \textrm{ (*1) } $$

Then we need to estimate $g(z)/(z(1-z))$ on the contour $\Omega_{\delta,\epsilon}$. We start with $U_{\delta,\epsilon}$.

If $z\in U_{\delta,\epsilon}$, then $\overline{z}\in D_{\delta,\epsilon}$. Thus, $$ \int_{D_{\delta,\epsilon}} + \int_{-U_{\delta,\epsilon}} = 2i\Im \int_{D_{\delta,\epsilon}}=e^{O(\delta)} \int_{\epsilon\cos \delta}^{1-\epsilon\cos\delta} 2i\sin (-\pi r+O(\delta|\log\epsilon|)) \frac1{r^{r+1}(1-r)^{2-r}} dr . \ \textrm{(*2)}$$ For $z\in L_{\delta,\epsilon}$, we have $$ g(z)=\exp(O(\epsilon |\log \epsilon |)). \ \textrm{(*3)} $$ Also for $z\in R_{\delta,\epsilon}$, we have $$ g(z)=\exp(O(\epsilon |\log\epsilon|)). \ \textrm{(*4)}$$ Thus, for integrals, we have $$ \int_{L_{\delta,\epsilon}} = (2\pi - 2\delta)i \exp(O(\epsilon |\log\epsilon|)), $$ and $$ \int_{R_{\delta,\epsilon}} = (2\pi - 2\delta)i \exp(O(\epsilon |\log\epsilon|)), $$ Letting $\delta\rightarrow 0+$, we obtain that $$ -2i \int_{\epsilon}^{1-\epsilon} (\sin \pi r) \frac1{r^{r+1}(1-r)^{2-r}} dr + 2 (2\pi )i \exp(O(\epsilon|\log\epsilon|))=0. $$ Letting $\epsilon\rightarrow 0+$, we obtain that $$ -2i \int_0^1 (\sin \pi r)\frac1{r^{r+1}(1-r)^{2-r}} dr + 2 \cdot 2\pi i =0. $$ Therefore, we have the desired result $$ \int_0^1 (\sin \pi r) \frac1{r^{r+1}(1-r)^{2-r}} dr = 2\pi. $$

Answer 3

For the proof, we will be using the following fact $$(1-\alpha)^{\left(\frac{1}{\alpha}-1\right)} = \int_0^1 \frac{\sin\left(\pi x \right)}{\pi (1-\alpha x)} \left[x^x\left(1-x\right)^{1-x}\right]^{-1}\ dx.$$

Taking your original sum, we have \begin{align} \int_0^1 \frac{x^{-1-x}(1-x)^{x-2}}{\Gamma(x)\Gamma(1-x)} dx &= \int_0^1 \frac{\sin(\pi x)}{\pi x(1-x)} \left[x^x\left(1-x\right)^{1-x}\right]^{-1} \ dx \\ &= \int_0^1 \frac{\sin(\pi x)}{\pi} \left[x^x\left(1-x\right)^{1-x}\right]^{-1} \left( \frac{1}{x}+\frac{1}{1-x}\right)\ dx \\ &=2\int_0^1 \frac{\sin(\pi x)}{\pi (1-x)} \left[x^x\left(1-x\right)^{1-x}\right]^{-1} \ dx \\ &= 2\lim_{\alpha \to 1^-} (1-\alpha)^{\left(\frac{1}{\alpha}-1\right)} =2\times 1 = 2 \end{align}